Cho tam giác ABC có góc A = 120^0, AB = 1, AC = 2. Trên tia CA kéo dài lấy điểm D sao cho BD = 2. Tính AD.

Hướng dẫn giải:

Đáp án đúng là: A.

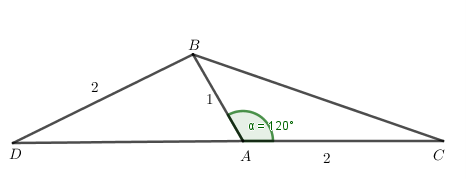
Ta có: \(\widehat {BAD} + \widehat {BAC} = 180^\circ \) (hai góc kề bù)

Suy ra: \(\widehat {BAD} = 180^\circ - \widehat {BAC} = 180^\circ - 120^\circ = 60^\circ \) nên cos\(\widehat {BAD} = \frac{1}{2}\).

Do đó áp dụng định lí côsin trong tam giác ABD, ta có:

\(\cos \widehat {BAD} = \frac{{A{D^2} + A{B^2} - B{D^2}}}{{2.AD.AB}}\)\( \Leftrightarrow \frac{1}{2} = \frac{{A{D^2} + {1^2} - {2^2}}}{{2.AD.1}}\)

\[ \Leftrightarrow A{D^2} - AD - 3 = 0\]

\( \Rightarrow AD = \frac{{1 + \sqrt {13} }}{2}\) (do AD > 0).