Cho hình thoi ABCD có cạnh bằng 2 cm và góc ABC = 60^0. Tìm khẳng định SAI trong các khẳng định sau? A. BD = 3 căn bậc hai 3 cm; B. góc BAD = 120^0; C. góc ADB = 30^0; D. AD = 2 cm...

Hướng dẫn giải:

Đáp án đúng là: A.

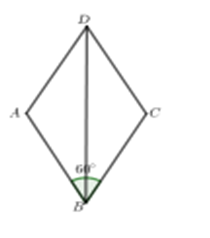
Vì \(\widehat {ABC} = 60^\circ \) nên \(\widehat {BAD} = 120^\circ \).

Ta có ABCD là hình thoi nên AB = AD = 2 cm.

Lại có BD là tia phân giác của góc \(\widehat {ABC}\) nên \(\widehat {ABD} = \frac{1}{2}\widehat {ABC} = \frac{1}{2}.60^\circ = 30^\circ \).

Mà AB = AD nên tam giác ABD cân tại A.

Do đó: \(\widehat {ADB} = \widehat {ABD} = 30^\circ \) và \(\widehat {BAD} = 180^\circ - 2\widehat {ABD} = 180^\circ - 2.30^\circ = 120^\circ \).

Áp dụng định lí côsin trong tam giác ABD ta có:

\(B{D^2} = A{B^2} + A{D^2} - 2.AB.AD.\cos \widehat {BAD}\)

Thay số: \(B{D^2} = {2^2} + {2^2} - 2.2.2.\cos 120^\circ = 12\)\( \Rightarrow BD = 2\sqrt 3 \)cm.