Trang chủ
Đề thi & kiểm tra
Lớp 10
Toán học
Trắc nghiệm Toán 10 CTST Bài 3. Giải tam giác và ứng dụng thực tế có đáp án !!
Từ vị trí điểm C người ta quan sát một...
Từ vị trí điểm C người ta quan sát một cây cao (như hình vẽ). Biết BC = 5 m, góc ACB = 45^0 , góc CBA = 50^0. Chiều cao của cây bằng bao nhiêu?
Câu hỏi :
Từ vị trí điểm C người ta quan sát một cây cao (như hình vẽ).
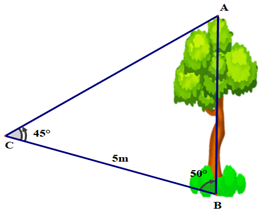
Biết BC = 5 m, \(\widehat {ACB} = 45^\circ ,\widehat {CBA} = 50^\circ \). Chiều cao của cây bằng bao nhiêu?
Từ vị trí điểm C người ta quan sát một cây cao (như hình vẽ).

Biết BC = 5 m, \(\widehat {ACB} = 45^\circ ,\widehat {CBA} = 50^\circ \). Chiều cao của cây bằng bao nhiêu?
* Đáp án
* Hướng dẫn giải
Hướng dẫn giải:
Áp dụng định lí tổng 3 góc trong tam giác, ta có: \(\widehat A + \widehat B + \widehat C = 180^\circ \)\( \Rightarrow \widehat A = 85^\circ \).
Theo định lí sin ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}}\)\( \Leftrightarrow \frac{{AB}}{{\sin 45^\circ }} = \frac{5}{{\sin 85^\circ }}\)\( \Leftrightarrow AB = \sin 45^\circ .\frac{5}{{\sin 85^\circ }}\)≈ 3,55 (m).
Vậy chiều cao của cây khoảng 3,55 m.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Trắc nghiệm Toán 10 CTST Bài 3. Giải tam giác và ứng dụng thực tế có đáp án !!
Số câu hỏi: 24
Copyright © 2021 HOCTAP247
