Từ hai điểm A và B của một tòa nhà, người ta quan sát điểm pháo hoa nổ. Biết rằng AB = 120 m, phương nhìn AC tạo với phương ngang một góc 45°, phương nhìn BC tạo với phương ngang g...
Câu hỏi :
Từ hai điểm A và B của một tòa nhà, người ta quan sát điểm pháo hoa nổ. Biết rằng AB = 120 m, phương nhìn AC tạo với phương ngang một góc 45°, phương nhìn BC tạo với phương ngang góc 15°30'.
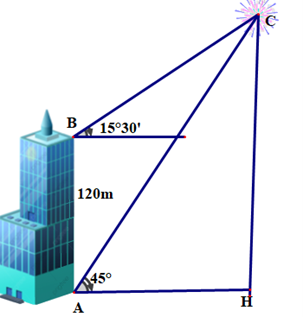
Hỏi điểm pháo hoa nổ cao so với mặt đất gần với giá trị nào sau đây?
Từ hai điểm A và B của một tòa nhà, người ta quan sát điểm pháo hoa nổ. Biết rằng AB = 120 m, phương nhìn AC tạo với phương ngang một góc 45°, phương nhìn BC tạo với phương ngang góc 15°30'.

Hỏi điểm pháo hoa nổ cao so với mặt đất gần với giá trị nào sau đây?
* Đáp án
* Hướng dẫn giải
Hướng dẫn giải:
Đáp án đúng là: A.
Ta có: \(\widehat {BAC} = \widehat {BAH} - \widehat {CAH} = 90^\circ - 45^\circ = 45^\circ \).
Lại có: \(\widehat {ABC} = 90^\circ + 15^\circ 30' = 105^\circ 30'\).
Trong tam giác ABC có: \(\widehat {BCA} = 180^\circ - \left( {\widehat {BAC} + \widehat {ABC}} \right) = 29^\circ 30'\).
Áp dụng định lí sin vào ∆ABC ta có:
\(\frac{{AC}}{{\sin \widehat {ABC}}} = \frac{{AB}}{{\sin \widehat {BCA}}}\)\( \Rightarrow \)AC = \(\sin \widehat {ABC}.\frac{{AB}}{{\sin \widehat {BCA}}}\)≈ 234,83 (m).
Trong tam giác vuông AHC có: \(\frac{{CH}}{{AC}} = \sin 45^\circ \)\( \Rightarrow \)CH = AC. sin 45° ≈ 166,05.
Vậy điểm pháo hoa nổ cao so với mặt đất khoảng 166,05 m.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Trắc nghiệm Toán 10 CTST Bài 3. Giải tam giác và ứng dụng thực tế có đáp án !!
Copyright © 2021 HOCTAP247
