Một xưởng sản xuất hai loại sản phẩm, mỗi kg sản phẩm loại I cần

Đáp án đúng là: A

Gọi x (x ≥ 0 (1)) là số kg loại I cần sản xuất, y (y ≥ 0 (2)) là số kg loại II cần sản xuất.

Số nguyên liệu cần dùng để sản xuất x sản phẩm loại I là: 2x

Số nguyên liệu cần dùng để sản xuất y sản phẩm loại II là: 4y

Xưởng có 200 kg nguyên liệu nên ta có: 2x + 4y ≤ 200 ⇔ x + 2y ≤ 100 ⇔ x + 2y – 100 ≤ 0 (3).

Thời gian để sản xuất x sản phẩm loại I là: 30x

Thời gian để sản xuất y sản phẩm loại II là: 15y

Xưởng có 1 200 giờ làm việc nên ta có: 30x + 15y ≤ 1200 hay 2x + y – 80 ≤ 0 (4)

Xét bất phương trình (1) và điểm A(1; 2) có:

Điểm A không nằm trên đường thẳng x = 0 và 1 ≥ 0, do đó, miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng có kể bờ x = 0 và chứa điểm A(1; 2).

Xét bất phương trình (2) và điểm B(0; 1) có:

Điểm B không nằm trên đường thẳng y = 0 và 1 ≥ 0, do đó, miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng có kể bờ y = 0 và chứa điểm B(0; 1).

Xét bất phương trình (3) và điểm (0; 0) ta có:

Điểm (0; 0) không nằm trên đường thẳng x + 2y – 100 = 0 và 0 + 2.0 – 100 = –100 < 0 nên miền nghiệm của bất phương trình (3) là nửa mặt phẳng có kể bờ x + 2y – 100 = 0 và chứa điểm (0; 0).

Xét bất phương trình (4) và điểm (0; 0) ta có:

Điểm (0; 0) không nằm trên đường thẳng 2x + y – 80 = 0 và 2.0 + 0 – 80 = –80 < 0 nên miền nghiệm của bất phương trình (4) là nửa mặt phẳng có kể bờ 2x + y – 80 = 0 và chứa điểm (0; 0).

Kết hợp miền nghiệm của các bất phương trình (1), (2), (3) và (4) là miền nghiệm thỏa mãn màu trắng trong hình vẽ:

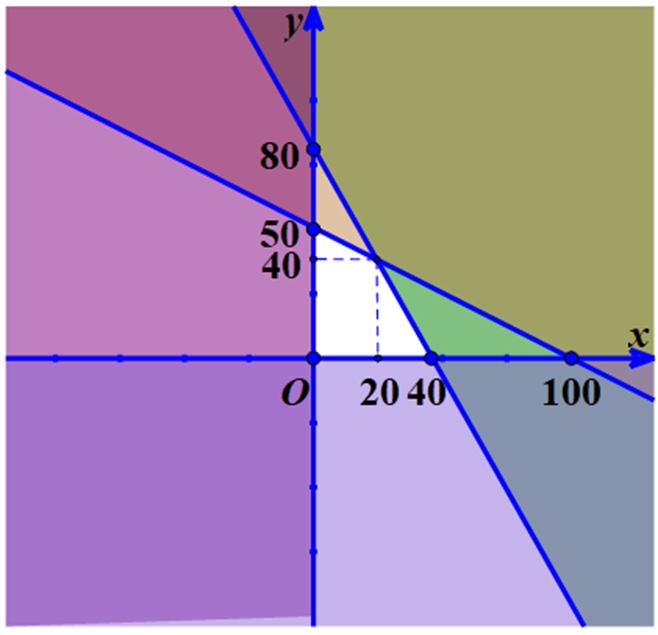
Lợi nhuận thu lại từ x sản phẩm loại I là: 40 000x

Lợi nhuận thu lại từ y sản phẩm loại II là: 30 000y

Tổng lợi nhuận là: 40 000x + 30 000y

Giá trị lớn nhất của L(x; y) = 40 000x + 30 000y đạt tại một trong các điểm (0; 0), (40; 0), (0; 50), (20; 40).

Ta có:

L(0; 0) = 0

L(40; 0) = 1 600 000

L(0; 50) = 1 500 000

L(20; 40) = 2 000 000

Vậy giá trị lớn nhất của L(x; y) là 2 000 000 khi (x; y) = (20; 40)

Vậy cần sản xuất 20kg sản phẩm loại I và 40kg sản phẩm loại II để có mức lợi nhuận lớn nhất.