Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit

Đáp án đúng là: D

Gọi x và y lần lượt là số kg thịt bò và thịt lợn mà gia đình đó mua mỗi ngày (0 ≤ x ≤ 1,6; 0 ≤ y ≤ 1,1)

Khi đó, chi phí để mua số thịt là: F(x; y) = 45x + 35y.

Trong x kg thịt bò có 800x đơn vị protein và 200x đơn vị lipit.

Trong y kg thịt lợn có 600y đơn vị protein và 400y đơn vị lipit.

Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày nên ta có hệ bất phương trình: 

$\left\{\begin{array}{l}800x+600y\ge 900\\ 200x+400y\ge 400\\ x\le 1,6\\ x\ge 0\\ y\le 1,1\\ y\ge 0\end{array}\right.\iff \left\{\begin{array}{l}8x+6y\ge 9\\ x+2y\ge 2\\ x\le 1,6\\ x\ge 0\\ y\le 1,1\\ y\ge 0\end{array}\right.$

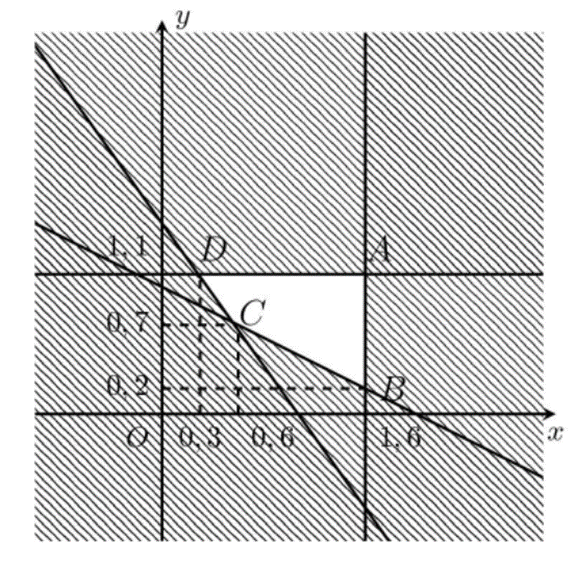
Miền nghiệm của hệ bất phương trình trên là miền tứ giác không bị gạch chéo trong hình vẽ (kể cả biên).

Ta có:

F(1,6; 1,1) = 45.1,6 + 35.1,1 = 110,5

F(1,6; 0,2) = 45.1,6 + 35.0,2 = 79

F(0,6; 0,7) = 45.0,6 + 35.0,7 = 51,5

F(0,3; 1,1) = 45.0,3 + 35.1,1 = 52

Vậy F(x; y) nhỏ nhất là 51,5 hay gia đình này cần phải mua 0,6 kg thịt bò và 0,7 kg thịt lợn để số tiền bỏ ra là ít nhất.