Một gia đình định trồng cà phê và ca cao trên diện tích 10 ha.

Câu hỏi :

Một gia đình định trồng cà phê và ca cao trên diện tích 10 ha. Nếu trồng cà phê thì cần 20 công và thu về 10 000 000 đồng trên diện tích mỗi ha, nếu trồng ca cao thì cần 30 công và thu 12 000 000 đồng trên diện tích mỗi ha. Hỏi cần trồng mỗi loại cây trên với diện tích là bao nhiêu để thu được nhiều tiền nhất. Biết rằng cà phê do các thành viên trong gia đình tự chăm sóc và số công không vượt quá 80, còn ca cao gia đình thuê người làm với giá 100 000 đồng cho mỗi công ?

* Đáp án

* Hướng dẫn giải

Đáp án đúng là: B

Gọi x và y lần lượt là số ha cà phê và ca cao mà hộ nông dân này trồng (x ≥ 0, y ≥ 0).

Số tiền cần bỏ ra để thuê người trồng ca cao là 30y.100 000 = 3 000 000y (đồng).

Lợi nhuận thu được là: F(x; y) = 10 000 000x + 12 000 000 – 3 000 000y = 10 000 000x + 9 000 000 y.

Vì số công để trồng cà phê không vượt quá 80 công và gia đình chỉ có 10 ha đất nên ta có hệ phương trình:

$\left\{\begin{array}{l}x+y\le 10\\ 20x\le 80\\ x\ge 0\\ y\ge 0\end{array}\right.\iff \left\{\begin{array}{l}x+y\le 10\\ x\le 4\\ x\ge 0\\ y\ge 0\end{array}\right.$

Miền nghiệm của hệ trên là miền tứ giác không bị gạch chéo trong hình vẽ (kể cả biên). F(x; y) đạt giá trị lớn nhất khi (x; y) là tọa độ của một trong các đỉnh tứ giác.

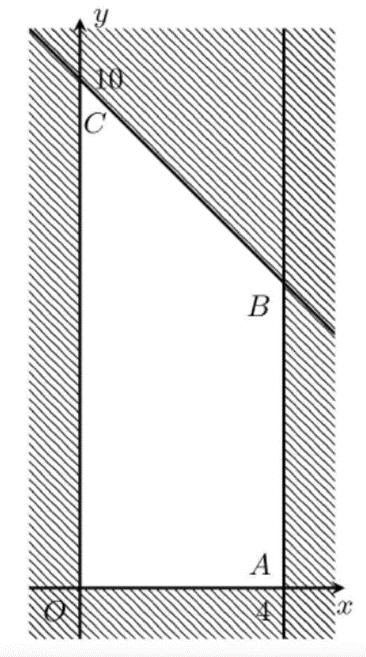
Ta có:

F(0; 0) = 0

F(4; 0) = 40 000 000

F(4; 6) = 94 000 000

F(0; 10) = 90 000 000

Vậy F(x; y) lớn nhất khi (x; y) = (4; 6) hay cần phải trồng 4 ha cà phê và 6 ha ca cao để thu về lợi nhuận lớn nhất.