Một phân xưởng có hai máy đặc chủng loại 1 và loại 2 sản xuất hai

Câu hỏi :

Một phân xưởng có hai máy đặc chủng loại 1 và loại 2 sản xuất hai loại sản phẩm kí hiệu là A và B. Một tấn sản phẩm loại A lãi 2 triệu đồng, một tấn sản phẩm loại B lãi 1,6 triệu đồng. Muốn sản xuất một tấn sản phẩm loại A phải dùng máy loại 1 trong 3 giờ và máy loại 2 trong 1 giờ. Muốn sản xuất một tấn sản phẩm loại B phải dùng máy loại 1 trong 1 giờ và máy loại 2 trong 1 giờ. Máy loại 1 làm việc không quá 6 giờ một ngày, máy loại 2 làm việc không quá 4 giờ 1 ngày. Hỏi cần sản xuất bao nhiêu tấn sản phẩm loại A và loại B để số tiền lãi mà phân xưởng này có thể thu được trong một ngày là lớn nhất?

* Đáp án

* Hướng dẫn giải

Đáp án đúng là: A

Gọi x, y lần lượt là số tấn sản phẩm loại A, B mà phân xưởng sản xuất trong 1 ngày (x ≥ 0, y ≥ 0).

Khi đó, số tiền lãi một ngày là: F(x; y) = 2x + 1,6y (triệu đồng).

Số giờ làm việc trong ngày của máy loại 1 là 3x + y.

Số giờ làm việc trong ngày của máy loại 2 là x + y.

Vì máy loại 1 làm việc không quá 6 giờ một ngày, máy loại 2 làm việc không quá 4 giờ 1 ngày nên ta có hệ phương trình $\left\{\begin{array}{l}3x+y\le 6\\ x+y\le 4\\ x\ge 0\\ y\ge 0\end{array}\right.$

Miền nghiệm của hệ phương trình là miền tứ giác không bị gạch trong hình vẽ.

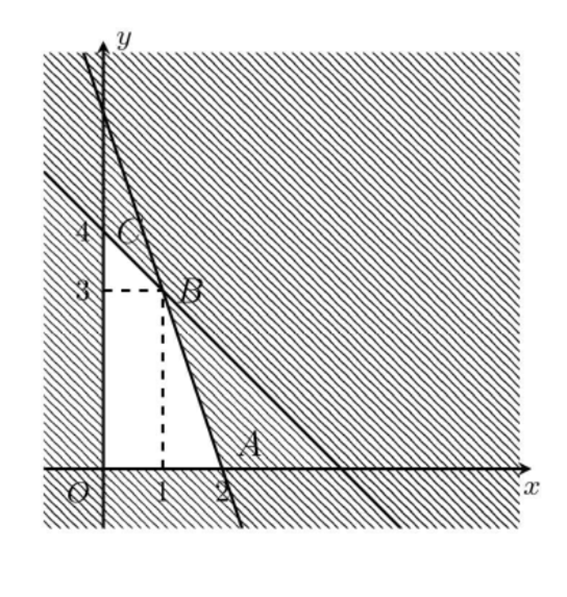
Ta có:

F(0; 0) = 0

F(2; 0) = 4

F(1; 3) = 6,8

F(0; 4) = 6,4

Do đó F(x; y) lớn nhất khi (x; y) = (1; 3).

Vậy để thu được lãi lớn nhất phải sản xuất 1 tấn sản phẩm loại A và 3 tấn sản phẩm loại B.