Cho tứ giác ABCD, I là trung điểm BD. Tìm điểm O thỏa mãn vecto OB+ 4 vecto OC= 2 vecto OD

Hướng dẫn giải:

Đáp án đúng là: B.

Ta có:

$\overrightarrow{OB}+4\overrightarrow{OC}=2\overrightarrow{OD}$

$\iff \overrightarrow{OB}+4\left(\overrightarrow{OB}+\overrightarrow{BC}\right)=2\left(\overrightarrow{OB}+\overrightarrow{BD}\right)$  (quy tắc ba điểm)

$\iff 3\overrightarrow{OB}=2\overrightarrow{BD}-4\overrightarrow{BC}$

$\iff 3\overrightarrow{OB}=2\left(\overrightarrow{BD}-\overrightarrow{BC}\right)-2\overrightarrow{BC}$   (quy tắc trừ hai vectơ)

$\iff 3\overrightarrow{OB}=2\overrightarrow{BD}-4\overrightarrow{BC}$

$\iff 3\overrightarrow{OB}=2\overrightarrow{BD}+4\overrightarrow{CB}$

$\iff 3\overrightarrow{OB}=2\left(\overrightarrow{CB}+\overrightarrow{BD}\right)+2\overrightarrow{CB}$

$\iff 3\overrightarrow{OB}=2\overrightarrow{CD}+2\overrightarrow{CB}$     (quy tắc ba điểm)

$\iff 3\overrightarrow{OB}=4\overrightarrow{CI}$       (do I là trung điểm của BD nên $\overrightarrow{CD}+\overrightarrow{CB}=2\overrightarrow{CI}$)

$\iff \overrightarrow{OB}=\frac{4}{3}\overrightarrow{CI}$

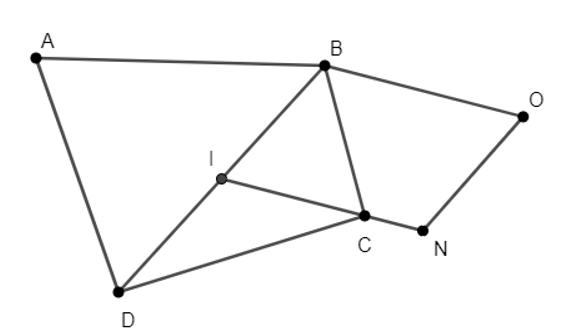
Vậy O là đỉnh của hình bình hành IBON với $\overrightarrow{IN}=\frac{4}{3}\overrightarrow{IC}$.