Cho hình bình hành ABCD. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AB và CD

Câu hỏi :

Cho hình bình hành ABCD. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AB và CD sao cho AB = 3AM, CD = 2CN và G là trọng tâm tam giác MNB. Phân tích vectơ $\overrightarrow{MN}$ qua các vectơ $\overrightarrow{AB}$ và $\overrightarrow{AC}$.

* Đáp án

* Hướng dẫn giải

Hướng dẫn giải:

Đáp án đúng là: C.

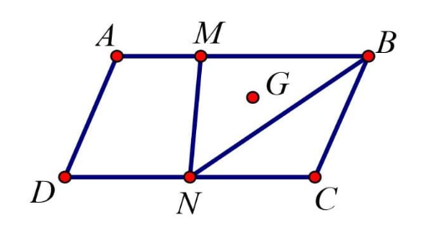
Vì AB = 3AM và M nằm trên cạnh AB nên $\overrightarrow{MA}=-\frac{1}{3}\overrightarrow{AB}$.

Ta có: $\overrightarrow{AN}=\overrightarrow{AC}+\overrightarrow{CN}=\overrightarrow{AC}-\frac{1}{2}\overrightarrow{AB}$ 

Do đó ta có: $\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AN}=-\frac{1}{3}\overrightarrow{AB}+\overrightarrow{AC}-\frac{1}{2}\overrightarrow{AB}=-\frac{5}{6}\overrightarrow{AB}+\overrightarrow{AC}$.