Số lượng học sinh đạt giải cuộc thi Học sinh giỏi tỉnh của 2 trường A và B từ năm
Câu hỏi :
Số lượng học sinh đạt giải cuộc thi Học sinh giỏi tỉnh của 2 trường A và B từ năm 2016 – 2021 được thống kê trong bảng dưới đây:
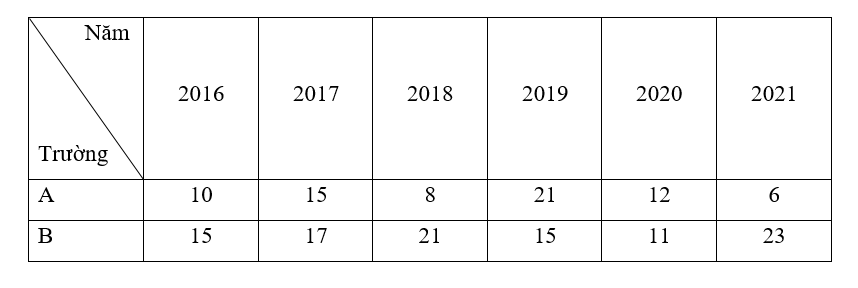
Sử dụng kiến thức về phương sai và độ lệch chuẩn, xác định xem số lượng học sinh đạt giải của trường nào ổn định hơn?
Số lượng học sinh đạt giải cuộc thi Học sinh giỏi tỉnh của 2 trường A và B từ năm 2016 – 2021 được thống kê trong bảng dưới đây:

Sử dụng kiến thức về phương sai và độ lệch chuẩn, xác định xem số lượng học sinh đạt giải của trường nào ổn định hơn?
* Đáp án
* Hướng dẫn giải
Hướng dẫn giải:
Đáp án đúng là: B.
- Số trung bình học sinh đạt giải trong các năm 2016 – 2021 của trường A là:
Công thức tính phương sai của một mẫu số liệu là:
S2 =
Thay số ta có:
= [(10 – 12)2 + (15 – 12)2 + (8 – 12)2 + (21 – 12)2 + (12 – 12)2 + (6 – 12)2] ≈ 24,33.
Do đó phương sai của mẫu số liệu trên là 24,33.
Độ lệch chuẩn của mẫu số liệu trên là SA = = ≈ 4,93.
- Số giờ trung bình sử dụng Internet của bạn Ngân là:
Công thức tính phương sai của một mẫu số liệu là:
S2 =
Thay số ta có:
= [(15 – 17)2 + (17 – 17)2 + (21 – 17)2 + (15 – 17)2 + (11 – 17)2 + (23 – 17)2 ] = 16.
Do đó phương sai của mẫu số liệu trên là 16.
Độ lệch chuẩn của mẫu số liệu trên là SB = = 4.
Ta thấy phương sai và độ lệch chuẩn trong số lượng học sinh đạt giải của trường B bé hơn trường A nên số lượng đạt giải của trường B ổn định hơn.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Trắc nghiệm Toán 10 CTST Bài 4. Các số đặc trưng đo mức độ phân tán của mẫu số liệu có đáp án !!
Copyright © 2021 HOCTAP247
