Cho tam giác ABC có trọng tâm G. Chứng minh các tam giác GBC, GAB, GAC có diện tích bằng nhau.

* Hướng dẫn giải

Lời giải

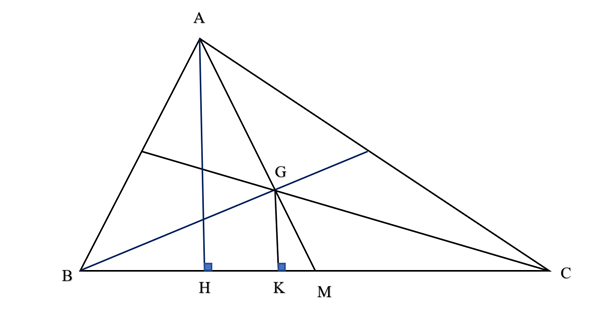
Vẽ AH và GK vuông góc với BC.

Gọi M là chân đường trung tuyến từ A hạ xuống BC. Ta có GM = \(\frac{1}{3}\)AM ( tính chất đường trung tuyến của tam giác).

Xét tam giác GKM và tam giác AHM:

\(\widehat {{\rm{AHM}}}\) = \(\widehat {{\rm{GKM}}}\) = 90°

\(\widehat {{\rm{AMH}}}\) = \(\widehat {{\rm{GMK}}}\)

⇒ tam giác GKM và tam giác AHM đồng dạng (g.g).

⇒ \(\frac{{{\rm{GM}}}}{{{\rm{AM}}}} = \frac{{{\rm{GK}}}}{{{\rm{AH}}}} = \frac{1}{3}\)

Có \(\frac{{{{\rm{S}}_{{\rm{GBC}}}}}}{{{{\rm{S}}_{{\rm{ABC}}}}}}{\rm{ = }}\frac{{\frac{{\rm{1}}}{{\rm{2}}}{\rm{.GK}}{\rm{.BC}}}}{{\frac{{\rm{1}}}{{\rm{2}}}{\rm{.AH}}{\rm{.BC}}}}\) = \(\frac{{{\rm{GK}}}}{{{\rm{AH}}}} = \frac{1}{3}\).

Chứng minh tương tự ta được:

S_GBC = S_GAB = S_GAC = \(\frac{1}{3}\)S_ABC. ( ĐPCM).