Để xác định chiều cao của một tòa nhà cao tầng, một người đứng tại điểm M, sử dụng giác kế nhìn thấy đỉnh tòa nhà với góc nâng góc RQA= 79°, người đó lùi ra xa một khoảng cách LM =...
Câu hỏi :
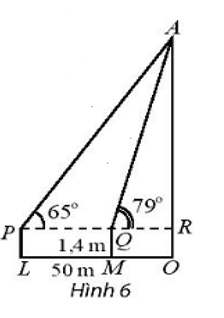
Để xác định chiều cao của một tòa nhà cao tầng, một người đứng tại điểm M, sử dụng giác kế nhìn thấy đỉnh tòa nhà với góc nâng \(\widehat {{\rm{RQA}}}\)= 79°, người đó lùi ra xa một khoảng cách LM = 50m thì nhìn thấy đỉnh tòa nhà với góc nâng \(\widehat {{\rm{RPA}}}\)= 65°. Hãy tính chiều cao của tòa nhà, biết rằng khoảng cách từ mặt đất đến ống ngắm của giác kế đó là PL = QM = 1,4 m ( Hình 6).
Để xác định chiều cao của một tòa nhà cao tầng, một người đứng tại điểm M, sử dụng giác kế nhìn thấy đỉnh tòa nhà với góc nâng \(\widehat {{\rm{RQA}}}\)= 79°, người đó lùi ra xa một khoảng cách LM = 50m thì nhìn thấy đỉnh tòa nhà với góc nâng \(\widehat {{\rm{RPA}}}\)= 65°. Hãy tính chiều cao của tòa nhà, biết rằng khoảng cách từ mặt đất đến ống ngắm của giác kế đó là PL = QM = 1,4 m ( Hình 6).

* Đáp án
* Hướng dẫn giải
Lời giải
Đặt d = PQ = 50m; h = AR là chiều cao từ giác kế đến đỉnh tòa nhà.
Ta có: \(\widehat {{\rm{RQA}}}\)= 79° và \(\widehat {{\rm{RPA}}}\)= 65°
tan\(\widehat {{\rm{RQA}}}\) = \(\frac{{{\rm{AR}}}}{{{\rm{QR}}}}\) = \(\frac{{\rm{h}}}{{{\rm{QR}}}}\) ⇒ QR = \(\frac{{\rm{h}}}{{{\rm{tan}}\widehat {{\rm{RQA}}}}}\) = \(\frac{{\rm{h}}}{{{\rm{tan79^\circ }}}}\).
tan\(\widehat {{\rm{RPA}}}\) = \(\frac{{{\rm{AR}}}}{{{\rm{PR}}}}\) = \(\frac{{\rm{h}}}{{{\rm{PR}}}}\) ⇒ PR = \(\frac{{\rm{h}}}{{{\rm{tan}}\widehat {{\rm{RPA}}}}}\) = \(\frac{{\rm{h}}}{{{\rm{tan65^\circ }}}}\).
Ta có:
PQ = PR – QR = \(\frac{{\rm{h}}}{{{\rm{tan65^\circ }}}}\) – \(\frac{{\rm{h}}}{{{\rm{tan79^\circ }}}}\) = h \(\left( {\frac{1}{{\tan 65^\circ }} - \frac{1}{{\tan 79^\circ }}} \right)\) = 50 (m)
⇒ h ≈ 183,9 (m)
Vậy chiều cao của tòa nhà là AR + RO ≈ 183,9 + 1,4 = 185,3 (m).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải SBT Toán 10 Bài 3. Giải tam giác và ứng dụng thực tế có đáp án !!
Copyright © 2021 HOCTAP247
