Cho tam giác ABC nội tiếp trong đường tròn (O). Gọi H là trực tâm tam giác ABC

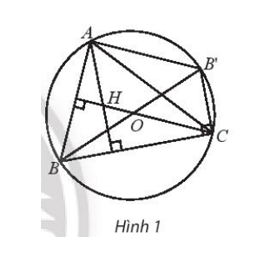
Do BB’ là đường kính nên $\widehat{\text{BCB'}}$ = 90° ( góc nội tiếp chắn nửa đường tròn )

⇒ BC ⊥ B’C.

H là trực tâm tam giác ABC nên BC ⊥ AH.

Suy ra AH // B’C ( do đều vuông góc với BC ).

Do BB’ là đường kính nên $\widehat{\text{BAB'}}$= 90° ( góc nội tiếp chắn nửa đường tròn )

⇒ BA ⊥ B’A.

H là trực tâm tam giác ABC nên CH ⊥ BA.

Suy ra CH // B’A ( do đều vuông góc với BA ).

Như vậy AB’CH là hình bình hành ( DHNB hình bình hành )

⇒ $\overrightarrow{\text{AH}}$ = $\overrightarrow{\text{B'C}}$ và $\overrightarrow{\mathrm{AB}\text{'}}$ = $\overrightarrow{HC}$.

Vậy $\overrightarrow{\text{AH}}$ = $\overrightarrow{\text{B'C}}$ và $\overrightarrow{\mathrm{AB}\text{'}}$ = $\overrightarrow{HC}$.