Trang chủ
Đề thi & kiểm tra
Lớp 10
Toán học
Giải SBT Toán 10 Bài tập cuối chương 5 có đáp án !!
Cho hình ngũ giác đều ABCDE tâm O. Chứng minh...
Cho hình ngũ giác đều ABCDE tâm O. Chứng minh rằng: vecto OA+OB+OC+OD+OE= vecto 0
Câu hỏi :
Cho hình ngũ giác đều ABCDE tâm O. Chứng minh rằng: .
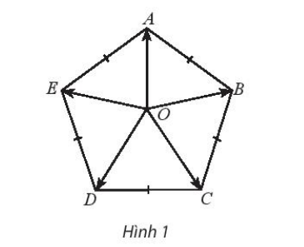
Cho hình ngũ giác đều ABCDE tâm O. Chứng minh rằng: .

* Đáp án
* Hướng dẫn giải
Đặt =
Ta có: =
Do OA nằm trên đường phân giác của và của hai tam giác cân BOE và DOC nên ta có các vectơ và nằm trên đường thẳng OA, suy ra nằm trên đường thẳng OA.
Chứng minh tương tự ta có cũng đồng thời nằm trên đường thẳng OB. Như vậy =
Vậy = .
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải SBT Toán 10 Bài tập cuối chương 5 có đáp án !!
Số câu hỏi: 45
Copyright © 2021 HOCTAP247
