Cho hệ bất phương trình 3x + 2y < 1 ( 1); x + 2/3y < 1( 2 ). Gọi S1 là miền nghiệm của bất phương trình (1), S2 là miền nghiệm của bất phương trình (2). Cho các phát biểu sau: (I)...

Hướng dẫn giải

Đáp án đúng là:

Ta có \(\left\{ \begin{array}{l}3x + 2y < 1\,\,\,\,\,\,\,\,\left( 1 \right)\\x + \frac{2}{3}y < 1\,\,\,\,\left( 2 \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x + 2y - 1 < 0\\3x + 2y - 3 < 0\end{array} \right.\)

Biểu diễn miền nghiệm của hệ \(\left\{ \begin{array}{l}3x + 2y - 1 < 0\\3x + 2y - 3 < 0\end{array} \right.\) trên mặt phẳng Oxy.

• Miền nghiệm của bất phương trình 3x + 2y – 1 < 0 là nửa mặt phẳng (kể cả bờ d₁: 3x + 2y – 1 = 0) chứa điểm O(0; 0).

• Miền nghiệm của bất phương trình 3x + 2y – 3 < 0 là nửa mặt phẳng (kể cả bờ d₂: 3x + 2y – 3 = 0) chứa điểm O(0; 0).

Miền không gạch chéo (kể cả bờ d₁, d₂) là giao của các miền nghiệm và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình đã cho.

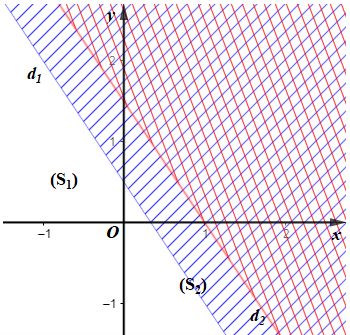
Do đó miền nghiệm của hệ bất phương trình là miền (S₁) nên chỉ có (I) đúng.

Vậy ta chọn phương án B.