Chương 1: Tứ Giác

Tìm x ở hình 5, hình 6:

Góc kề bù với một góc của tứ giác gọi là góc ngoài của tứ giác.

a) Tính các góc ngoài của tứ giác ở hình 7a.

b) Tính tổng các góc ngoài của tứ giác ở hình 7b (tại mỗi đỉnh của tứ giác chỉ chọn một góc ngoài) : + ++=?

c) Có nhận xét gì về tổng các góc ngoài của tứ giác?

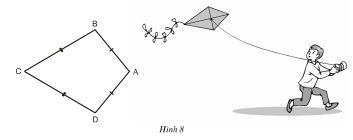
Ta gọi tứ giác ABCD trên hình 8 có AB = AD, CB = CD là hình "cái diều"

a) Chứng minh rằng AC là đường trung trực của BD.

b) Tính \(\widehat{B}, \widehat{D}\) biết rằng \(\widehat{A}= 100^0\) và \(\widehat{C}= 60^0\) .

Dựa vào cách vẽ các tam giác đã học, hãy vẽ lại các tứ giác ở hình 9, hình 10 vào vở.

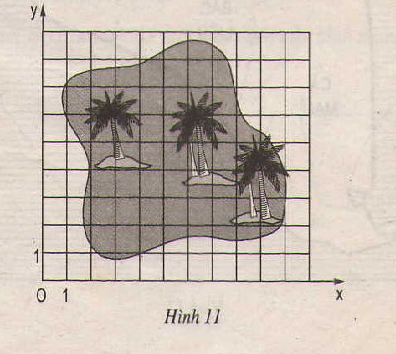
Đố. Đố em tìm thấy vị trí của "kho báu" trên hình 11, biết rằng kho báu nằm tại giao điểm các đường chéo của tứ giác ABCD, trong đó các đỉnh của tứ giác có tọa độ như sau: A(3 ; 2), B(2 ; 7), C(6 ; 8), D(8 ; 5).

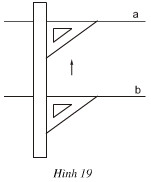
Dùng thước và êke, ta có thể kiểm tra được hai đường thẳng có song song với nhau hay không (xem hình 19). Trên hình 20, có những tứ giác nào là hình thang, có những tứ giác nào không là hình thang. Bằng cách nêu trên, hãy kiểm tra xem trong các tứ giác ở hình 20, tứ giác nào là hình thang

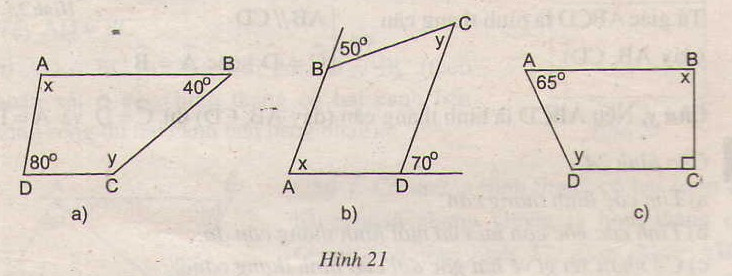
Tìm x và y trên hình 21, biết rằng ABCD là hình thang có đáy là AB và CD.

Hình thang ABCD (AB // CD) có \(\widehat{A}-\widehat{D}=20^0,\)​. Tính các góc của hình thang.

Đố hình 22 là hình vẽ một chiếc thang trên hình vẽ có bao nhiêu hình thang?

Tính độ dài các cạnh của hình thang cân ABCD trên giấy kẻ ô vuông (h.30, độ dài cạnh ô vuông là 1cm).

Cho hình thang cân ABCD ( AB // CD, AB < CD). Kẻ đường cao AE, BF của hình thang. Chứng minh rằng DE = CF.

Cho hình thang cân ABCD (AB // CD), E là giao điểm của hai đường chéo. Chứng minh rằng EA = EB, EC = ED.

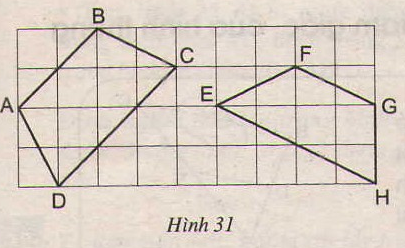
Đố. Trong các tứ giác ABCD và EFGH trên giấy kẻ ô vuông (h.31), tứ giác nào là hình thang cân? Vì sao?

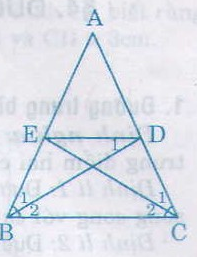
Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy theo thứ tự các điểm D và E sao cho AD = AE.

a) Chứng minh rằng BDEC là hình thang cân.

b) Tính các góc của hình thang cân đó, biết rằng \(\widehat{A}=50^0\)

Cho tam giác ABC cân tại A, các đường phân giác BD, CE (D ∈ AC, E ∈ AB). Chứng minh rằng BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.

Hình thang ABCD (AB // CD) có \(\widehat{ACD}=\widehat{BDC}\). Chứng minh rằng ABCD là hình thang cân.

Chứng minh định lí "Hình thang có hai đường chéo bằng nhau là hình thang cân" qua bài toán sau: Cho hình thang ABCD (AB = CD) có AC = BD.

Qua B kẻ đường thẳng song song với AC, cắt đường thẳng DC tại E. Chứng mình rằng:

a) ∆BDE là tam giác cân.

b) \(\Delta ACD = \Delta BDC\)​.

c) Hình thang ABCD là hình thang cân.

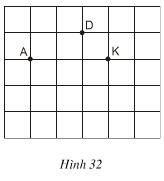
Đố. Cho ba điểm A, D, K trên giấy kẻ ô vuông (h.32). Hãy tìm điểm thứ tư M là giao điểm của các dòng kẻ sao cho nó cùng với ba điểm đã cho là bốn đỉnh của một hình thang cân

.

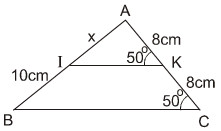
Tìm x trên hình 41.

Tính khoảng cách AB giữa hai mũi của compa trên hình 42, biết rằng C là trung điểm của OA, D là trung điểm của OB và OD = 3cm.

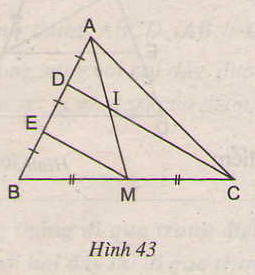
Cho hình 43. Chứng minh rằng AI = IM.

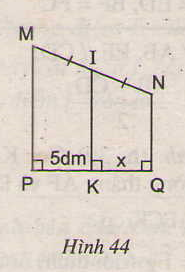
Tìm x trên hình 44,

Hai điểm A và B thuộc cùng một nửa mặt phẳng có bờ là đường xy. Khoảng cách từ điểm A đến xy bằng 12cm, khoảng cách từ điểm B đến xy bằng 20cm. Tính khoảng cách từ trung điểm C của AB đến xy.

Hình thang ABCD có đáy AB, CD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, BD. Chứng minh ba điểm E, K, F thẳng hàng.

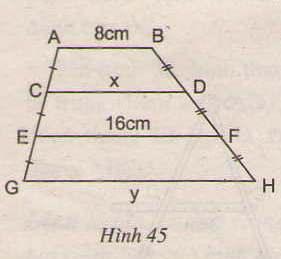
Tính x, y trên hình 45, trong đó AB // CD // EF // GH.

Cho tứ giác ABCD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, AC.

a) So sánh các độ dài EK và CD, KF và AB.

b) Chứng minh rằng \(EF \leq \frac{AB+CD}{2}\)

Cho hình thang ABCD (AB // CD), E là trung điểm của AD, F là trung điểm của BC. Đường thằng EF cắt BD ở I, cắt AC ở K.

a) Chứng minh rằng AK = KC, BI = ID.

b) Cho AB = 6cm, CD = 10cm. Tính các độ dài EI, KF, IK.

Dựng tam giác ABC vuông tại A, biết cạnh huyền \(BC = 4cm\), góc nhọn \(\widehat{B}=65^0\)

Dựng tam giác ABC vuông tại B, biết cạnh huyền AC = 4cm, cạnh góc vuông BC = 2cm.

Dựng hình thang ABCD (AB // CD), biết AB = AD = 2cm, AC = DC = 4cm.

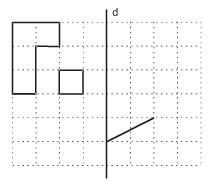
Vẽ hình đối xứng với cá hình đã cho qua trục d (h.58).

Cho góc xOy có số đo 50⁰, điểm A nằm trong góc đó. Vẽ điểm B đối xứng với A qua Ox, vẽ điểm C đối xứng với A qua Oy.

a) So sánh các độ dài OB và OC.

b) Tính số đo góc BOC.

Tìm các hình có trục đối xứng trên hình 59.

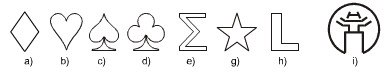
Thực hành. Cắt một tấm bìa hình tam giác cân, một tấm bìa hình thang cân. Hãy cho biết đường nào là trục đối xứng của mỗi hình, sau đó gấp mỗi tấm bìa để kiểm tra lại điều đó.

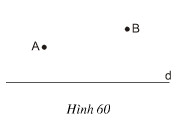
a) Cho hai điểm A, B thuộc cùng một nửa mặt phẳng có bờ là đường thẳng d (h.60). Gọi C là điểm đối xứng với A qua d. Gọi D là giao điểm của đường thẳng d và đoạn thẳng BC. Gọi E là điểm bất kì của đường thẳng d (E khác D).

Chứng minh rằng AD + DB < AE + EB.

b) Bạn Tú đang ở vị trí A, cần đến bờ sông d lấy nước rồi đi đến vị trí B (h.60). Con đường ngắn nhất mà bạn Tú nên di là con đường nào?

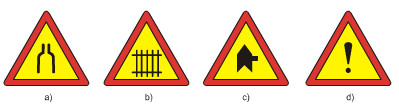
Trong các biển báo giao thông sau đấy, biển nào có trục đối xứng ?

a) Biển nguy hiểm: đường hẹp hai bên (h.61a)

b) Biển nguy hiểm: đường giao với đường sắt có rào chắn (h.61b)

c) Biển nguy hiểm: đường ưu tiên gặp đường không ưu tiên bên phải (h.61c)

d) Biên nguy hiểm khác (h.61d)

Các câu sau đúng hay sai ?

a) Nếu ba điểm thẳng hàng thì ba điểm đối xứng với chúng qua một trục cũng thẳng hàng.

b) Hai tam giác đối xứng với nhau qua một trục thì có chu vi bằng nhau.

c) Một đường tròn có vô số trục đối xứng.

d) Một đoạn thẳng chỉ có một trục đối xứng.

Đố.

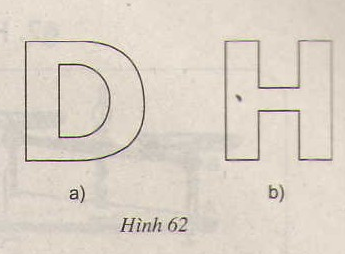
a) Hãy tập cắt chứ D (h. 62a) bằng cách gấp đôi tờ giấy. Kể tên một vài chữ cái khác (kiểu chứ in hoa) có trục đối xứng.

b) Vì sao ta có thể gấp tờ giấy làm tư để cắt chứ H (h. 62b) ?

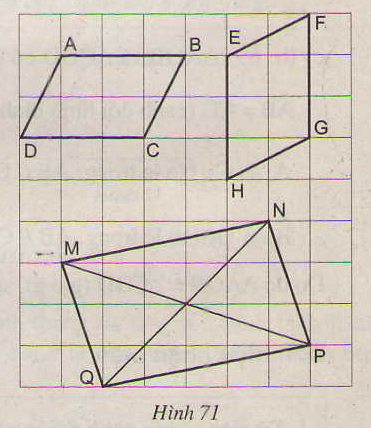
Các tứ giác ABCD, EFGH, MNPQ trên giấy kẻ ô vuông ở hình 71 có là hình bình hành hay không ?

Cho hình bình hành ABCD. Gọi  E là trung điểm của AD, F là trung điểm của BC. Chứng minh rằng BE = DF.

Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB ở E, tia phân giác của góc B cắt CD ở F.

a) Chứng minh rằng DE // BF.

b) Tứ giác DEBF là hình gì? Vì sao ?

Các câu sau đúng hay sai ?
a) Hình thang có hai cạnh đáy bằng nhau là hình bình hành.

b) Hình thang có hai cạnh bên song song là hình bình hành.

c) Tứ giác có hai cạnh đối bằng nhau là hình bình hành.

d) Hình thang có hai cạnh bên bằng nhau là hình bình hành.

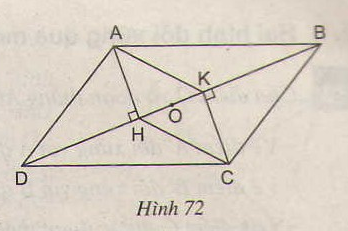
Cho hình 72, trong đó ABCD là hình bình hành.

a) Chứng minh rằng AHCK là hình bình hành.

b) Gọi O là trung điểm của HK. Chứng minh rằng ba điểm A, O, C thẳng hàng

Tứ giác ABCD có E, F, G, H theo thứ tự là trung  điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì ? Vì sao ?

Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB. Đường chéo BD cắt AI, CK theo thứ tự ở M và N. Chứng minh rằng:

a) AI // CK

b) DM = MN = NB

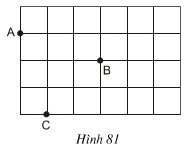
Vẽ điểm A' đối xứng với A qua B, vẽ điểm C đối xứng với C qua B (h.81).

Trong mặt phẳng tọa độ, cho điểm H có tọa độ (3; 2). Hãy vẽ điểm K đối xứng với H qua gốc tọa độ và tìm tọa độ K.

Cho hình bình hành ABCD. Gọi E là điểm đối xứng với D qua điểm A, gọi F là điểm đối xứng với D qua điểm C. Chứng minh rằng điểm E đối xứng với điểm F qua điểm B.

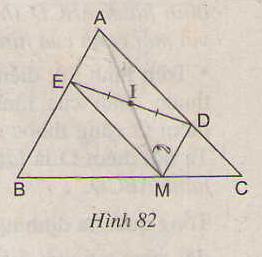
Cho hình 82, trong đó MD // AB và ME // AC. Chứng minh rằng điểm A đối xứng với  điểm M qua I. 

Cho góc vuông xOy, điểm A nằm trong góc đó. Gọi B là điểm đối xứng với A qua Ox, gọi C là điểm đối xứng với A qua Oy. Chứng mình rằng điểm B đối xứng với điểm C qua O.

Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Một đường thẳng đi qua O cắt các cạnh AB và CD theo thứ tự ở M và N. Chứng minh rằng điểm M đối xứng với điểm N qua O.

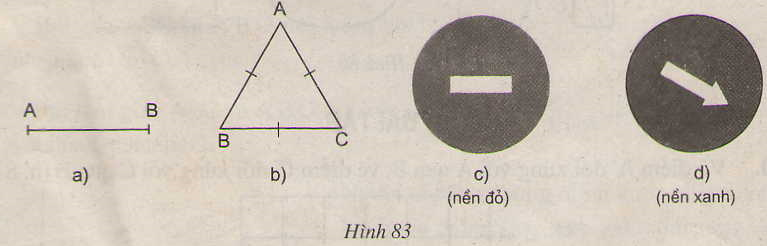
Trong các hình vẽ sau, hình nào có tâm đối xứng ?

a) Đoạn thẳng AB (h.83a);

b) Tam giác đếu ABC (h.83b);

c) Biển cấm đi ngược chiều (h.83c);

d) Biển chỉ hướng đi vòng tránh chướng ngại vật (h.83d)

Các câu sau đúng hay sai ?

a) Tâm đối xứng của một đường thẳng là điểm bất kì của đường thẳng đó.

b) Trọng tâm của một tam giác là tâm đối xứng của tam giác đó.

c) Hai tam giác đối xứng với nhau qua một điểm thì có chu vi bằng nhau.

Điền vào chỗ trống, biết rằng a, b là độ dài các cạnh, d là độ dài đường chéo của một hình chứ nhật.

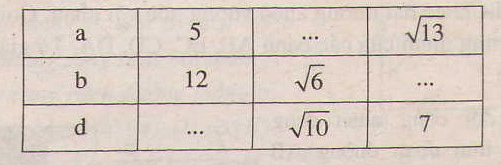
Chứng minh rằng:
a) Giao điểm hai đường chéo cuẩ hình chữ nhật là tâm đối xứng củahình chữ nhật đó.

b) Hai đường thẳng đi qua trung điểm hai cặp cạnh đối của hình chữ nhật là hai trục đối xứng của hình chữ nhật đó.

Tính độ dài đường trung tuyến ứng với cạnh huyền của một tam giác vuông có các cạnh góc vuông bằng 7cm và 24cm.

Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC, E là điểm đối xứng với H qua I. Tứ giác AHCE là hình gì ? Vì sao ?

Các câu sau đúng hay sai ?

a) Nếu tam giác ABC vuông tại C thì điểm C thuộc đường tròn có đường kính là AB (h.88)

b) Nếu điểm C thuộc đường tròn có đường kính là AB (C khác A và B) thì tam giác ABC vuông tại C(h.89).

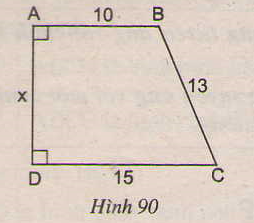
Tìm x trên hình 90.

Tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì ? Vì sao ?

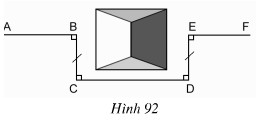
Đố. Một đội công nhân đang trồng cây trên đoạn đường AB thì gặp chướng ngại vật che lấp tầm nhìn (h.92). Đội đã dựng các điểm C, D, E như trên hình vẽ rồi trồng cây tiếp trên đoạn thẳng EF vuông góc với DE. Vì sao AB và EF cùng nằm trên một đường thẳng ?

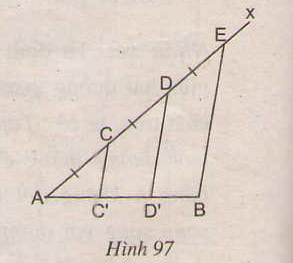
Cho đoạn thẳng AB. Kẻ tia Ax bất kì. Trên tia Ax lấy các điểm C, D, E sao cho AC = CD = DE (h.97). Kẻ đoạn thẳng EB. Qua C, D kẻ các đường thẳng song song với EB. Chứng minh rằng đoạn thẳng AB bị chia ra ba phần bằng nhau.

Cho điểm A nằm ngoài đường thẳng d và có khoảng cách đến d bằng 2cm lấy điểm B bất kì thuộc đường thằng d. Gọi C là điểm đối xứng với điểm A qua điểm B. Khi điểm B di chuyển trên đường thẳng d thì điểm C di chuyển trên đường nào ?

Ghép mỗi ý (1), (2), (3), (4) với một trong các ý (5), (6), (7), (8) để được một khẳng định đúng:

(1) Tập hợp các điểm cách điểm A cố định một khoảng 3cm

(2) Tập hợp các điểm cách đều hai đầu của đoạn thẳng AB cố định

(3) Tập hợp các điểm nằm trong góc xOy và cách đều hai cạnh của góc đó

(4) Tập hợp các điểm cách đều đường thẳng a cố định một khoảng 3cm

(5) là đường trung trực của đoạn thẳng AB.

(6) la hai đường thẳng song song với a và cách a một khoảng 3cm

(7) là đường tròn tâm A bán kính 3cm.

(8) là tia phân giác của góc xOy.

Cho góc vuông xOy, điểm A thuộc tia Oy sao cho OA = 2cm. Lấy B là một điểm bất kì thuộc tia Ox. Gọi C là trung điểm của AB. KHi điểm B di chuyển trên tia Ox thì điểm C di chuyển trên đường nào?

Cho tam giác ABC vuông tại A. Lấy M là một điểm bất kì thuộc cạnh BC. Gọi MD là đường vuông góc kẻ từ M đến AB, ME là đường vuông góc kẻ từ M đến AC, O là trung điểm của DE.

a) Chứng mình rằng ba điểm A, O, M thằng hàng.

b) Khi điểm M di chuyển trên cạnh BC thì điểm O di chuyển trên đường nào?

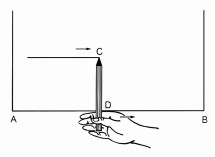
Đố. Để vạch một đường thẳng song song với mép gỗ 10cm, bác thợ mộc đặt đoạn bút chì CD dài 10cm vuông góc với ngón tay trỏ lấy làm cữ (h.98), rồi đưa ngón trỏ chạy dọc theo mép gỗ AB. Căn cứ vào kiến thức nào mà ta kết luận được rằng đầu chì C vạch nên đường thẳng song song với AB và cách AB là 10cm ?

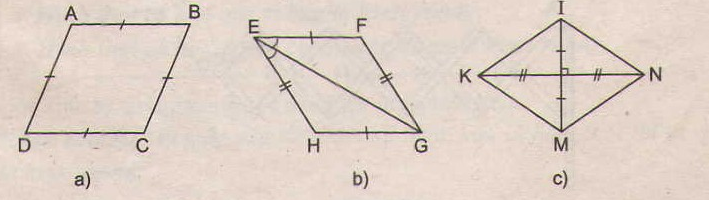
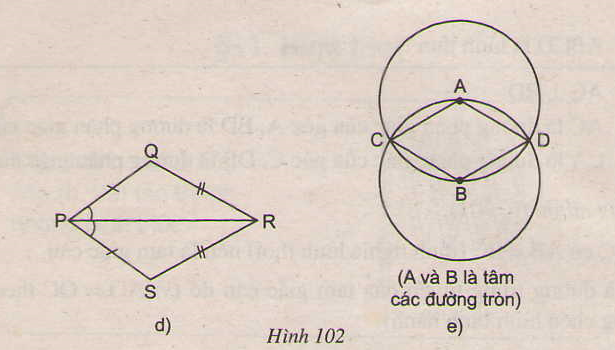
Tìm các hình thoi trên hình 102.

Hai đường chéo của một hình thoi bằng 8cm và 10cm. Cạnh của hình thoi bằng giá trị nào trong các giá trị sau:

(A) \(6cm\)                    (B) \(\sqrt{41} cm\)                  (C) \(\sqrt{164} cm\)              (D) \(9cm\) 

Chứng minh rằng các trung điểm của bốn cạnh của một hình chữ nhật là các đỉnh của hình thoi.

Chứng minh rằng các trung điểm của bốn cạnh của một hình thoi là các đỉnh của một hình chữ nhật.

Chứng minh rằng:

a) Giao điểm hai đường chéo của hình thoi là tâm đối xứng của hình thoi.

b) Hai đường chéo của hình thoi là hai trục đối xứng của hình thoi.

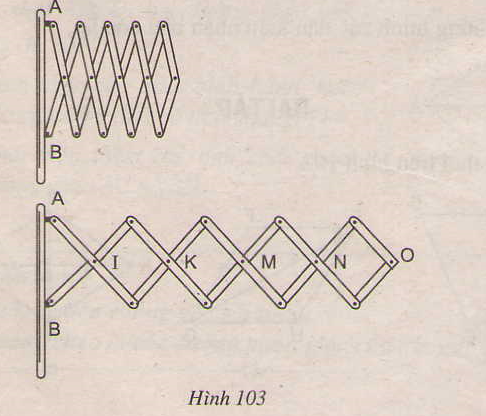
Đố. Hình 103 biểu diễn một phần của cửa xếp, gồm những thanh kim loại dài bàng nhau và được liên kết với nhau bởi các chốt tại hai đầu và tại trung điểm. Vì sao tại mỗi vị trí của cửa xếp, các tứ giác trên hình vẽ đều là hình thoi, các điểm chốt I, K, M, N, O nằm trên một đường thẳng ?

a) Một hình vuông có cạnh bằng 3cm. Đường chéo của hình vuông đó bằng 6cm,  cm, 5cm hay 4cm ?

b) Đường  chéo của một hình vuông bằng 2dm. Cạnh cảu hình vuông đó bằng: 1dm, dm, dm hay dm ?

Hãy chỉ rõ tâm đối xứng của hình vuông, các trục đối xứng của hình vuông.

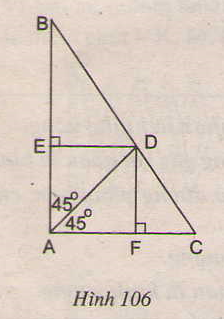
Cho hình 106. Tứ giác AEDF là hình gì? Vì sao?

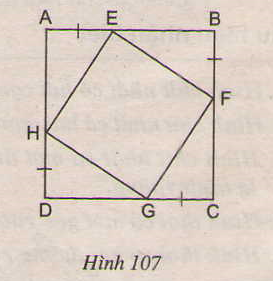
Cho hình 107, trong đó ABCD là hình vuông. Chứng minh rằng tứ giác EFGH là hình vuông.

Các câu sau đúng hay sai ?

a) Tứ giác có hai đường chéo vuông góc với nhau là hình thoi.

b) Tứ giác có hai đường chéo vuông góc nhau tại trung điểm của mỗi đường là hình thoi.

c) Hình thoi là tứ giác có tất cả các cạnh bằng nhau.

d) Hình chữ nhật có hai đường chéo bằng nhau là hình vuông.

e) Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.

Cho tam giác ABC, D là điểm nằm giữa B và C. Qua D kẻ các đường thẳng song song với AB và AC, chúng cắt các cạnh AC và AB theo thứ tự ở E và F.

a) Tứ giác AEDF là hình gi ? Vì sao ?

b) Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình thoi ?

c) Nếu tam giác ABC vuông tại A thì tứ giác AEDF là hình gì ? Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình vuông ?

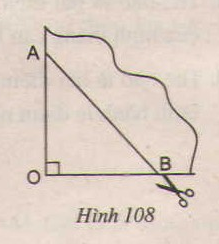
Đố. Lấy một tờ giấy gấp làm tư rồi cắt chéo theo nhát cắt AB (h.108). Sau khi mở tờ giấy ra, ta được một tứ giác. Tứ giác nhận được là hình gì ? Vì sao ? Nếu ta có OA = OB thì tứ giác nhận được là hình gì ?