Bài tập 71 trang 103 SGK Toán 8 Tập 1
Bài tập 71 trang 103 SGK Toán 8 Tập 1
Cho tam giác ABC vuông tại A. Lấy M là một điểm bất kì thuộc cạnh BC. Gọi MD là đường vuông góc kẻ từ M đến AB, ME là đường vuông góc kẻ từ M đến AC, O là trung điểm của DE.
a) Chứng mình rằng ba điểm A, O, M thằng hàng.
b) Khi điểm M di chuyển trên cạnh BC thì điểm O di chuyển trên đường nào?
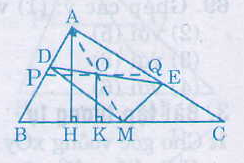
Câu a:
Tứ giác ADME có\(\widehat{A}=\widehat{D}=\widehat{E}=90^0\)
nên ADME là hình chữ nhật
O là trung điểm của đường chéo AM.
Vậy A, O, M thẳng hàng
Câu b:
Kẻ AH ⊥ BC. Tương tự như bài 77 ta có hai cách chứng minh như sau:
Vì O là trung điểm của AM nên HO là trung tuyến ứng với cạnh huyền AM. Do đó OA = OH. Suy ra điểm O di chuyển trên đường trung trực của AH.
Mặt khác vì M di chuyển trên đoạn PQ. Vậy điểm O di chuyển trên đoạn thẳng PQ là đường trung bình của ABC.
-- Mod Toán 8
Copyright © 2021 HOCTAP247
