Bài tập 49 trang 93 SGK Toán 8 Tập 1
Lý thuyết
Bài tập
Câu hỏi:
Bài tập 49 trang 93 SGK Toán 8 Tập 1
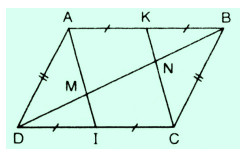
Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB. Đường chéo BD cắt AI, CK theo thứ tự ở M và N. Chứng minh rằng:
a) AI // CK
b) DM = MN = NB
Câu a:
Tứ giác ABCD có AB = CD, AD = BC nên là hình bình hành.
Tứ giác AICK có AK // IC, AK = IC nên là hình bình hành.
Do đó AI // CK
Câu b:
∆DCN có DI = IC, IM // CN.
(vì AI // CK) nên suy ra DM = MN
Chứng minh tương tự đối với ∆ABM ta có MN = NB.
Vậy DM = MN = NB
-- Mod Toán 8
Copyright © 2021 HOCTAP247
