Bài tập 3 trang 67 SGK Toán 8 Tập 1
Lý thuyết
Bài tập
Câu hỏi:
Bài tập 3 trang 67 SGK Toán 8 Tập 1
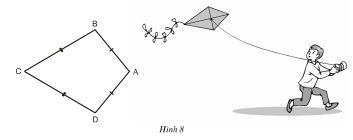
Ta gọi tứ giác ABCD trên hình 8 có AB = AD, CB = CD là hình "cái diều"
a) Chứng minh rằng AC là đường trung trực của BD.
b) Tính \(\widehat{B}, \widehat{D}\) biết rằng \(\widehat{A}= 100^0\) và \(\widehat{C}= 60^0\) .
Câu a:
Ta có: AB = AD (gt) ⇒ A thuộc đường trung trực của BD
CB = CD (gt) ⇒ C thuộc đường trung trực của BD.
Vậy AC là đường trung trực của BD.
Câu b:
Xét ∆ ABC và ∆ADC có AB = AD (gt)
BC = DC (gt)
AC cạnh chung
nên ∆ ABC = ∆ADC (c.c.c)
Suy ra: \(\widehat{B}= \widehat{D}\)
Ta có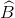 
+ 
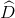= 3600 – (1000 + 600) = 2000
Do đó \(\widehat{B}= \widehat{D}= 100^0\)
-- Mod Toán 8
Copyright © 2021 HOCTAP247