Bài tập 54 trang 96 SGK Toán 8 Tập 1
Bài tập 54 trang 96 SGK Toán 8 Tập 1
Cho góc vuông xOy, điểm A nằm trong góc đó. Gọi B là điểm đối xứng với A qua Ox, gọi C là điểm đối xứng với A qua Oy. Chứng mình rằng điểm B đối xứng với điểm C qua O.
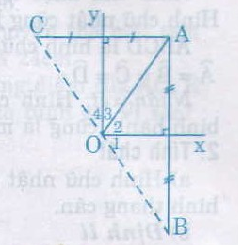
Cách 1:
B đối xứng với A qua Ox nên Ox là đường trung trực của AB ⇒ OA = OB
C đối xứng với A qua Oy nên OY là đường trung trực của AC ⇒ OA = OC
Suy ra OB = OC (1)
∆AOB cân tại O ⇒ =
=
∆AOC cân tại O ⇒ =
=
Mà \(\widehat{AOB}+\widehat{AOC}=2(\widehat{O_2}+\widehat{O_3}) =2.90^0=180^0\)
⇒ B, O, C thẳng hàng (2)
Từ (1) và (2) suy ra B đối xứng với C qua O.
Cách 2:
A đối xứng với B qua Ox và O nằm trên Ox nên OA đối xứng với OB qua OX suy ra
OA = OB.
A đối xứng với C qua Oy và O nằm trren Oy nên OA đối xứng với OC qua Oy.
Suy ra OA = OC
Do đó OB = OC (1)
và \(\widehat{AOB}+\widehat{AOC}=2(\widehat{O_2}+\widehat{O_3}) =2.90^0=180^0\)
⇒ B, O, C thẳng hàng (2)
Từ (1) và (2) suy ra B đối xứng với C qua O.
-- Mod Toán 8
Copyright © 2021 HOCTAP247
