Bài tập 82 trang 108 SGK Toán 8 Tập 1

Bài tập 82 trang 108 SGK Toán 8 Tập 1

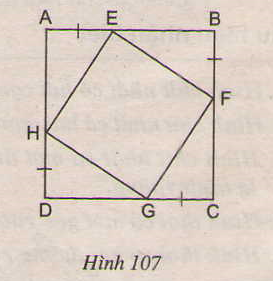
Các tam giác vuông AEH, BFC, CGF, DHG có:

AE = BF = CG = DH (gt)

Suy ra AH = BE = CF = DG

Nên  ∆AEH =  ∆BFE =  ∆CGF =  ∆DHG (c.g.c)

Do đó HE = EF = FG = GH                        (1)

và  = 

Ta có \(\widehat{HEF}= 180^0 -\)  ( + \(\widehat{FEB} = 180^0 -\))( + )

                     = 180⁰ - 90⁰ = 90⁰   (2)

Từ (1) và (2) ta được EFGH là hình vuông

-- Mod Toán 8