Bài tập 45 trang 92 SGK Toán 8 Tập 1
Bài tập 45 trang 92 SGK Toán 8 Tập 1
Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB ở E, tia phân giác của góc B cắt CD ở F.
a) Chứng minh rằng DE // BF.
b) Tứ giác DEBF là hình gì? Vì sao ?
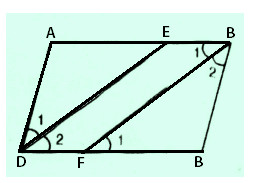
Câu a:
Ta có :
\(\widehat{B}=\widehat{D}\) (Vì ABC D là hình hành)
\(\widehat{B_1}=\widehat{B_2}=\frac{\widehat{B}}{2}\) (BF là tia phân giác góc B)
\(\widehat{D_1}=\widehat{D_2}=\frac{\widehat{D}}{2}\) (DE là tia phân giác góc D)
⇒\(\widehat{D_2}=\widehat{B_1}\) (1)
Ta lại có AB // CD (Vì ABCD là hình bình hành)
Cũng có nghĩa BE // CF
⇒\(\widehat{B_1}=\widehat{F_1}\) (2) (Vì là 2 góc so le trong)
Mà \(\widehat{D_1},\widehat{F_1}\) là cặp góc đồng vị
Do đó DE // BF ( có hai góc đồng vị bằng nhau)
Câu b:
Tứ giác DEBF có:
DE // BF (chứng minh ở câu a)
BE // DF (vì AB // CD)
Nên theo đình nghĩa DEBF là hình bình hành.
-- Mod Toán 8
Copyright © 2021 HOCTAP247
