Bài tập 27 trang 80 SGK Toán 8 Tập 1
Lý thuyết
Bài tập
Câu hỏi:
Bài tập 27 trang 80 SGK Toán 8 Tập 1
Cho tứ giác ABCD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, AC.
a) So sánh các độ dài EK và CD, KF và AB.
b) Chứng minh rằng \(EF \leq \frac{AB+CD}{2}\)
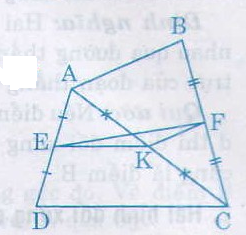
Câu a:
Trong ∆ACD có EA = ED, KA = KC (gt)
nên EK là đường trung bình của ∆ACD
Do đó EK =
Tương tự KF là đường trung bình của ∆ABC.
Nên KF =
Câu b:
Ta có EF ≤ EK + KF (bất đẳng thức trong ∆EFK)
Nên EF ≤ EK + KF = +
=
Vậy \(EF \leq \frac{AB+CD}{2}\)
-- Mod Toán 8
Copyright © 2021 HOCTAP247
