Bài tập 1 trang 156 SBT Toán 9 Tập 1
Lý thuyết
Bài tập
Câu hỏi:
Bài tập 1 trang 156 SBT Toán 9 Tập 1
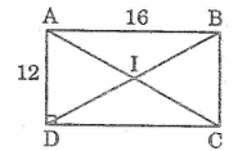
Cho hình chữ nhật ABCD có AD = 12cm, CD = 16cm. Chứng minh rằng bốn điểm ABCD cùng thuộc một đường tròn.Tính bán kính của đường tròn đó.
Gọi I là giao điểm của hai đường chéo AC và BD. Ta có:
IA = IB = IC = ID (tính chất hình chữ nhật)
Vậy bốn điểm A, B, C, D cùng nằm trên một đường tròn bán kính AC/2
Áp dụng định lí Pitago vào tam giác vuông ABC ta có:
AC2 = AB2 + BC2 = 162 + 122 = 256 + 144 = 400
Suy ra: AC = √400 = 20 (cm)
Vậy bán kính đường tròn là: IA = AC/2 = 20/2 = 10 (cm)
-- Mod Toán 9
Copyright © 2021 HOCTAP247