Bài tập 16 trang 159 SBT Toán 9 Tập 1
Lý thuyết
Bài tập
Câu hỏi:
Bài tập 16 trang 159 SBT Toán 9 Tập 1
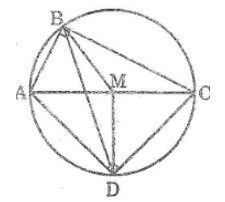
Tứ giác ABCD có \(\widehat B = \widehat D = {90^0}\)
a. Chứng minh rằng bốn điêm A, B, C, D cùng thuộc một đường tròn
b. So sánh độ dài AC và BD. Nếu AC = BD thì tứ giác ABCD là hình gì?
Tam giác ABC vuông tại B có BM là đường trung tuyến nên:
BM = (1/2).AC (tính chất tam giác vuông)
Tam giác ACD vuông tại D có DM là đường trung tuyến nên:
DM = (1/2).AC (tính chất tam giác vuông)
Suy ra: MA = MB = MC = MD
Vậy bốn điểm A, B, C, D cùng nằm trên một đường tròn tâm M bán kính bằng (1/2).AC.
b. Trong đường tròn tâm M ta có BD là dây cung không đi qua tâm, AC là đường kính nên: BD < AC
AC = BD khi và chỉ khi BD là đường kính. Khi đó tứ giác ABCD là hình chữ nhật.
-- Mod Toán 9
Copyright © 2021 HOCTAP247