Bài tập 48 trang 164 SBT Toán 9 Tập 1
Bài tập 48 trang 164 SBT Toán 9 Tập 1
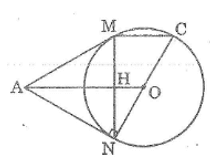
Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AM, AN với đường tròn (M, N là các tiếp điểm)
a. Chứng minh rằng OA ⊥ MN
b. Vẽ đường kính NOC. Chứng minh rằng MC // AO
c. Tính độ dài các cạnh của tam giác AMN biết OM = 3cm, OA = 5cm
a. Ta có: AM = AN (tính chất hai tiếp tuyến cắt nhau)
Suy ra tam giác AMN cân tại A
Mặt khác AO là đường phân giác của góc MAN (tính chất hai tiếp tuyến cắt nhau)
Suy ra AO là đường cao của tam giác AMN (tính chất tam giác cân)
Vậy OA ⊥ MN.
b. Tam giác MNC nội tiếp trong đường tròn (O) có NC là đường kính nên góc (CMN) = 90o
Suy ra: NM ⊥ MC
Mà OA ⊥ MN (chứng minh trên)
Suy ra: OA // MC
c. Ta có: AN ⊥ NC (tính chất tiếp tuyến)
Áp dụng định lí Pitago vào tam giác vuông AON ta có:
AO2 = AN2 + ON2
Suy ra : AN2 = AO2 – ON2 = 52 – 32 = 16
AN = 4 (cm)
Suy ra: AM = AN = 4 (cm)
Gọi H là giao điểm của AO và MN
Ta có: MH = NH = MN/2 (tính chất tam giác cân)
Tam giác AON vuông tại N có NH ⊥ AO. Theo hệ thức lượng trong tam giác vuông, ta có:
OA.NH = AN.ON ⇒ NH = (AN.ON)/AO = (4.3)/5 = 2,4 (cm)
MN = 2.NH = 2.2,4 = 4,8 (cm)
-- Mod Toán 9
Copyright © 2021 HOCTAP247