Trang chủ Đề thi & kiểm tra Lớp 10 Toán học Đề kiểm tra giữa học kì 2 Toán 10 có đáp án (Mới nhất) !! Cho tam thức bậc hai f(x) = ã^2 + bx...

Cho tam thức bậc hai f(x) = ã^2 + bx + c (a khác 0) có Delta = b^2 - 4ac > 0. Gọi x1; x2 ( x1 < x2) là hai nghiệm

Câu hỏi :

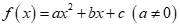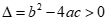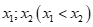Cho tam thức bậc hai Cho tam thức bậc hai f(x) = ã^2 + bx + c (a khác 0) có Delta = b^2 - 4ac > 0. Gọi x1; x2 ( x1 < x2) là hai nghiệm (ảnh 1)  có Cho tam thức bậc hai f(x) = ã^2 + bx + c (a khác 0) có Delta = b^2 - 4ac > 0. Gọi x1; x2 ( x1 < x2) là hai nghiệm (ảnh 2) . Gọi Cho tam thức bậc hai f(x) = ã^2 + bx + c (a khác 0) có Delta = b^2 - 4ac > 0. Gọi x1; x2 ( x1 < x2) là hai nghiệm (ảnh 3)  là hai nghiệm phân biệt của 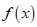Cho tam thức bậc hai f(x) = ã^2 + bx + c (a khác 0) có Delta = b^2 - 4ac > 0. Gọi x1; x2 ( x1 < x2) là hai nghiệm (ảnh 4) . Chọn mệnh đề đúng trong các mệnh đề sau.

A. Cho tam thức bậc hai f(x) = ã^2 + bx + c (a khác 0) có Delta = b^2 - 4ac > 0. Gọi x1; x2 ( x1 < x2) là hai nghiệm (ảnh 5) luôn cùng dấu với hệ số a khi Cho tam thức bậc hai f(x) = ã^2 + bx + c (a khác 0) có Delta = b^2 - 4ac > 0. Gọi x1; x2 ( x1 < x2) là hai nghiệm (ảnh 6).


B. Cho tam thức bậc hai f(x) = ã^2 + bx + c (a khác 0) có Delta = b^2 - 4ac > 0. Gọi x1; x2 ( x1 < x2) là hai nghiệm (ảnh 7) luôn cùng dấu với hệ số a khi Cho tam thức bậc hai f(x) = ã^2 + bx + c (a khác 0) có Delta = b^2 - 4ac > 0. Gọi x1; x2 ( x1 < x2) là hai nghiệm (ảnh 8) hoặc Cho tam thức bậc hai f(x) = ã^2 + bx + c (a khác 0) có Delta = b^2 - 4ac > 0. Gọi x1; x2 ( x1 < x2) là hai nghiệm (ảnh 9).



C. Cho tam thức bậc hai f(x) = ã^2 + bx + c (a khác 0) có Delta = b^2 - 4ac > 0. Gọi x1; x2 ( x1 < x2) là hai nghiệm (ảnh 10) luôn âm với mọi Cho tam thức bậc hai f(x) = ã^2 + bx + c (a khác 0) có Delta = b^2 - 4ac > 0. Gọi x1; x2 ( x1 < x2) là hai nghiệm (ảnh 11)



D. Cho tam thức bậc hai f(x) = ã^2 + bx + c (a khác 0) có Delta = b^2 - 4ac > 0. Gọi x1; x2 ( x1 < x2) là hai nghiệm (ảnh 12) luôn dương với mọi Cho tam thức bậc hai f(x) = ã^2 + bx + c (a khác 0) có Delta = b^2 - 4ac > 0. Gọi x1; x2 ( x1 < x2) là hai nghiệm (ảnh 13)


* Đáp án

* Hướng dẫn giải

Chọn đáp án B

Theo định lí về dấu của tam thức bậc hai.

Câu hỏi trên thuộc đề trắc nghiệm dưới đây !

Đề kiểm tra giữa học kì 2 Toán 10 có đáp án (Mới nhất) !!

Số câu hỏi: 263

Lớp 10

Toán học

Toán học - Lớp 10

Home
Tiểu học Lớp 6 Lớp 7 Lớp 8 Lớp 9 Lớp 10 Lớp 11 Lớp 12 Hóa học Tài liệu Đề thi & kiểm tra Câu hỏi hoctapsgk.com Nghe truyện audio Đọc truyện chữ Công thức nấu ăn

Copyright © 2021 HOCTAP247