Cho đường thẳng ∆ có phương trình tổng quát ax + by + c = 0 (a hoặc b khác 0). Nêu nhận xét về vị trí tương đối của đường thẳng ∆ với các trục tọa độ trong mỗi trường hợp sau: a) b...

Hướng dẫn giải

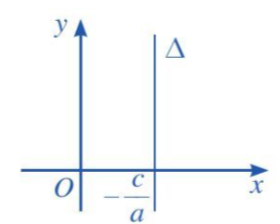
a) Nếu b = 0 và a ≠ 0 thì phương trình đường thẳng ∆ trở thành ax + c = 0.

Khi đó đường thẳng ∆ song song hoặc trùng với trục Oy và cắt trục Ox tại điểm \(\left( { - \frac{c}{a};\,0} \right)\)

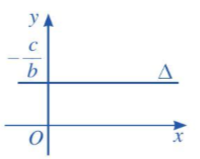
b) Nếu b ≠ 0 và a = 0 thì phương trình đường thẳng ∆ trở thành by + c = 0.

Khi đó đường thẳng ∆ song song hoặc trùng với trục Ox và cắt trục Oy tại điểm \(\left( {0;\, - \frac{c}{b}} \right)\)

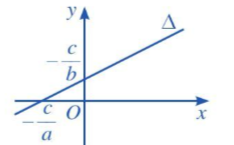
c) Nếu b ≠ 0 và a ≠ 0 thì phương trình đường thẳng ∆ có thể viết thành

\(y = - \frac{a}{b}x - \frac{c}{b}\).

Khi đó, đường thẳng ∆ là đồ thị hàm số bậc nhất \(y = - \frac{a}{b}x - \frac{c}{b}\) với hệ số góc \(k = - \frac{a}{b}\).