Bài tập Phương trình đường thẳng có đáp án !!
Câu 9 : B. Bài tập
Câu 18 :
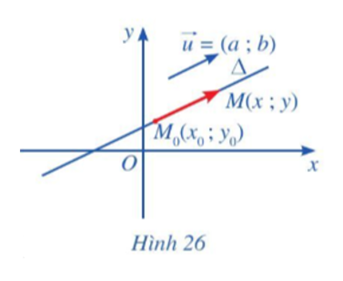
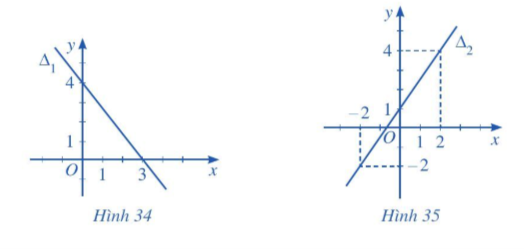
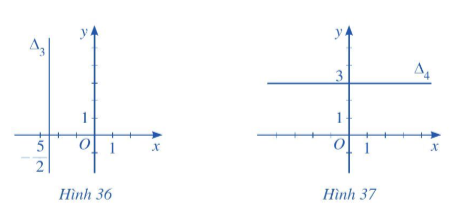
Chỉ ra tọa độ của hai điểm thuộc Δ.
Câu 24 :
Đường trung trực cạnh AB.
Đường trung trực cạnh AB.
Câu 27 :
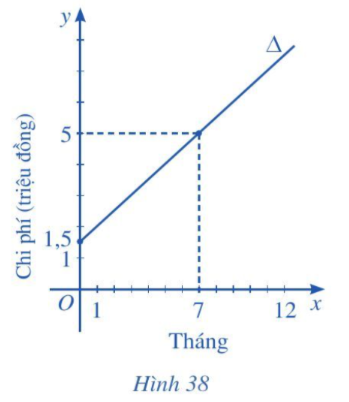
Tính tổng chi phí mà người đó phải trả khi tham gia phòng tập thể dục với thời gian 12 tháng.
Tính tổng chi phí mà người đó phải trả khi tham gia phòng tập thể dục với thời gian 12 tháng.
Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).
Copyright © 2021 HOCTAP247