Trang chủ
Đề thi & kiểm tra
Lớp 10
Toán học
Trắc nghiệm Toán 10 Bài 6. Hệ thức lượng trong tam giác có đáp án !!
Hình bình hành ABCD có AB = a; BC =...
Hình bình hành ABCD có AB = a; BC = a căn bậc hai 2 và góc BAD = 45 độ
Câu hỏi :
Hình bình hành ABCD có AB = a; \(BC = a\sqrt 2 \) và \(\widehat {BAD} = 45^\circ \). Khi đó hình bình hành có diện tích bằng
Hình bình hành ABCD có AB = a; \(BC = a\sqrt 2 \) và \(\widehat {BAD} = 45^\circ \). Khi đó hình bình hành có diện tích bằng
A. 2a2;
B. \({a^2}\sqrt 2 \);
C. a2;
D. \({a^2}\sqrt 3 \).
* Đáp án
* Hướng dẫn giải
Đáp án đúng là: C
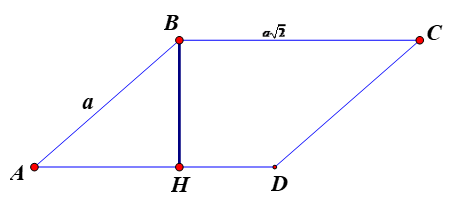
Gọi BH là đường cao của hình bình hành ABCD.
Tam giác BAH vuông tại H, góc \(\widehat {BAH} = \widehat {BAD} = 45^\circ \),
Ta có BH = AB.sin45° = \(\frac{{a\sqrt 2 }}{2}\).
Diện tích hình bình hành ABCD là: \(S = BH.AD = \frac{{a\sqrt 2 }}{2}.a\sqrt 2 = {a^2}\)(đvdt).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Trắc nghiệm Toán 10 Bài 6. Hệ thức lượng trong tam giác có đáp án !!
Số câu hỏi: 15
Copyright © 2021 HOCTAP247
