Cho tam giác ABC có M là trung điểm của AB, N là trung điểm của AC
Câu hỏi :
Cho tam giác ABC có M là trung điểm của AB, N là trung điểm của AC và P là trung điểm của BC.
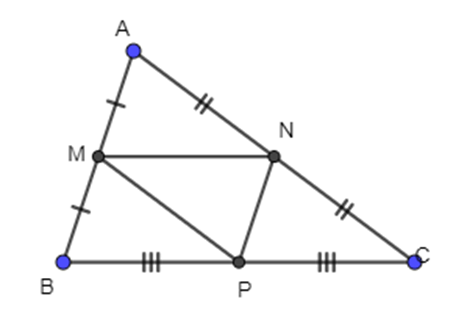
Phát biểu nào dưới đây là sai.
Cho tam giác ABC có M là trung điểm của AB, N là trung điểm của AC và P là trung điểm của BC.

Phát biểu nào dưới đây là sai.
A. \(\overrightarrow {MN} = \overrightarrow {PC} \);
B. \(\overrightarrow {AA} \) cùng hướng với \(\overrightarrow {PP} \);
C. \(\overrightarrow {MB} = \overrightarrow {AM} \);
D. \(\overrightarrow {MN} = \overrightarrow {PB} \).
* Đáp án
* Hướng dẫn giải
Đáp án đúng là D
+) Xét tam giác ABC, có:
M là trung điểm AB
N là trung điểm của AC
⇒ MN là đường trung bình của tam giác ABC
⇒ MN // BC và MN = \(\frac{1}{2}\)BC
Mà BP = PC = \(\frac{1}{2}\)BC (P là trung điểm của BC)
⇒ MN = CP = PB (1)
Vì MN // BC nên MN // CP. Khi đó \(\overrightarrow {MN} \) và \(\overrightarrow {PC} \) cùng phương. Suy ra \(\overrightarrow {MN} \) và \(\overrightarrow {PC} \) cùng hướng (2)
Từ (1) và (2) suy ra \(\overrightarrow {MN} \) = \(\overrightarrow {CP} \). Do đó đáp án A đúng.
Tương tự MN //BC hay MN // PB. Khi đó \(\overrightarrow {MN} \) và \(\overrightarrow {PB} \) cùng phương nhưng ngược hướng (3)
Từ (1) và (3) suy ra \(\overrightarrow {MN} \) không bằng \(\overrightarrow {PB} \). Do đó đáp án D sai.
+) Ta có \(\overrightarrow {AA} \) và \(\overrightarrow {PP} \) là các vectơ – không.
Mà mọi vectơ – không có cùng độ dài và cùng hướng nên bằng nhau
Suy ra \(\overrightarrow {AA} \) cùng hướng với \(\overrightarrow {PP} \). Do đó đáp án B đúng.
+) Hai vec tơ \(\overrightarrow {AM} \) và \(\overrightarrow {MB} \) cùng hướng
Vì M là trung điểm của AB nên AM = MB
Suy ra \(\overrightarrow {AM} = \overrightarrow {MB} \). Do đó đáp án C đúng.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Trắc nghiệm Toán 10 Bài 7. Khái niệm vectơ có đáp án !!
Copyright © 2021 HOCTAP247
