Cho tam giác ABC vuông cân tại A, đường cao AH và BC = 10cm.
Câu hỏi :
Cho tam giác ABC vuông cân tại A, đường cao AH và BC = 10cm. Tính độ dài vectơ \(\overrightarrow {AB} + \overrightarrow {AC} \).
Cho tam giác ABC vuông cân tại A, đường cao AH và BC = 10cm. Tính độ dài vectơ \(\overrightarrow {AB} + \overrightarrow {AC} \).
A. 5cm;
B. 10dm;
C. 10cm;
D. 15cm.
* Đáp án
* Hướng dẫn giải
Đáp án đúng là C
Xét tam giác ABC vuông cân tại A có AH là đường cao nên AH là đường trung tuyến suy ra H là trung điểm của BC.
Gọi D là điểm đối xứng với A qua H.
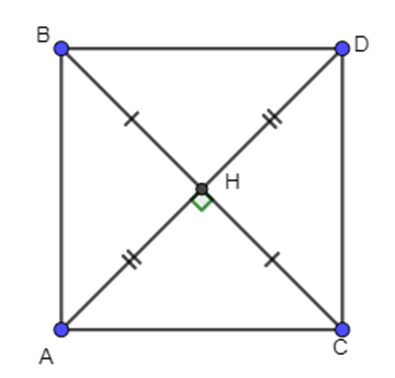
Xét tứ giác ABDC có AD cắt BC tại H là trung điểm của mỗi đường. Do đó ABDC là hình bình hành.
⇒ \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \) (quy tắc hình bình hành)
⇒ \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right|\)
Ta lại có hình bình hành ABDC có \(\widehat {BAC} = {90^0}\) nên ABDC là hình chữ nhật do đó AD = BC =10 cm.
⇒ \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD = BC = 10cm\).
Vậy độ dài \(\overrightarrow {AB} + \overrightarrow {AC} \) là 10 cm.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Trắc nghiệm Toán 10 Bài 8. Tổng và hiệu của hai vectơ có đáp án !!
Copyright © 2021 HOCTAP247
