Cho hình thoi ABCD có độ dài cạnh bằng 2 dm và góc BAD = 100 độ.

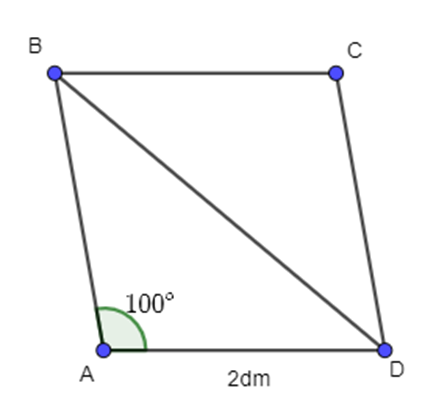
Vì ABCD là hình thoi nên ABCD là hình bình hành khi đó: \(\overrightarrow {DA} + \overrightarrow {DC} = \overrightarrow {DB} \) (quy tắc hình bình hành)

Xét tam giác ABD có:

BD² = AB² + AD² – 2.AB.AD.cos\(\widehat {BAD}\)

⇔ BD² = 2² + 2² – 2.2.2.cos100°

⇔ BD² = 2² + 2² – 2.2.2.cos100°

⇔ BD² ≈ 9,39

⇔ BD ≈ 3,06 dm

⇒ \(\left| {\overrightarrow {DA} + \overrightarrow {DC} } \right| = \left| {\overrightarrow {DB} } \right| = 3,06\,\,dm.\)

Vậy độ dài vectơ \(\overrightarrow {DA} + \overrightarrow {DC} \) là 3,06 dm.