Cho hình bình hành ABCD có tâm O, G là trọng tâm tam giác BCD

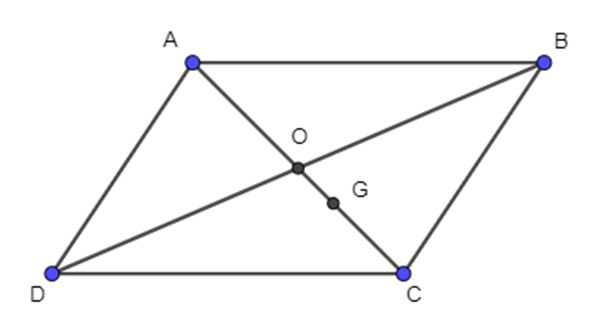
+) Ta có \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \) (quy tắc hình bình hành). Do đó A đúng.

+) Vì G là trọng tâm tam giác BCD nên \(\overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \). Do đó B đúng.

+) O là tâm của hình bình hành ABCD nên O là trung điểm của AC. Suy ra \(\overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow 0 \). Do đó C đúng.

+) Vì G là trọng tâm tam giác BCD nên GC = 2GA. Suy ra \(\overrightarrow {GC} + \overrightarrow {GO} \ne \overrightarrow 0 \). Do đó D sai.