Hai người cùng kéo một con thuyền với hai lực vecto F1 = vecto OA
Câu hỏi :
Hai người cùng kéo một con thuyền với hai lực \[\overrightarrow {{F_1}} = \overrightarrow {OA} ,\,\,\overrightarrow {{F_2}} = \overrightarrow {OB} \] có độ lớn lần lượt là 550 N, 800 N. Cho biết góc giữa hai vectơ là 52o.
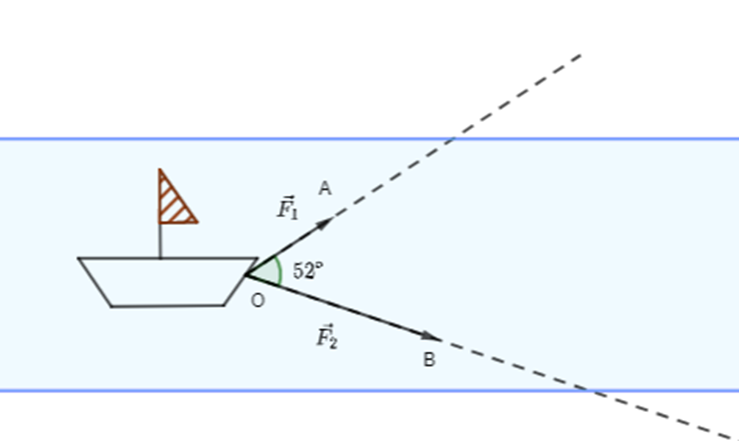
Độ lớn của vectơ hợp lực \[\overrightarrow F \] là tổng của hai lực \[\overrightarrow {{F_1}} \] và \[\overrightarrow {{F_2}} \] nằm trong khoảng nào dưới đây?
Hai người cùng kéo một con thuyền với hai lực \[\overrightarrow {{F_1}} = \overrightarrow {OA} ,\,\,\overrightarrow {{F_2}} = \overrightarrow {OB} \] có độ lớn lần lượt là 550 N, 800 N. Cho biết góc giữa hai vectơ là 52o.

Độ lớn của vectơ hợp lực \[\overrightarrow F \] là tổng của hai lực \[\overrightarrow {{F_1}} \] và \[\overrightarrow {{F_2}} \] nằm trong khoảng nào dưới đây?
A. (900; 1 000);
B. (1 000; 1 100);
C. (1 100; 1 200);
D. (1 200; 1 300).
* Đáp án
* Hướng dẫn giải
Đáp án đúng là D
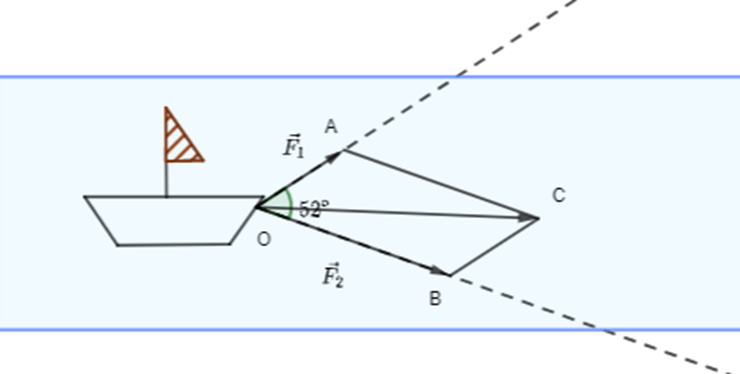
Dựng hình bình hành AOBC.
Khi đó \[\overrightarrow F = \overrightarrow {OC} \].
Do AOBC là hình bình hành nên \[\widehat {AOB} + \widehat {OBC} = 180^\circ \] và OA = BC = 550.
Do đó \[\widehat {OBC} = 180^\circ - \widehat {AOB} = 180^\circ - 52^\circ = 128^\circ \].
Áp dụng định lí côsin vào tam giác OBC có:
OC2 = OB2 + BC2 - 2.OB.BC.cos \[\widehat {OBC}\]
\[ \Rightarrow \] OC2 = 8002 + 5502 - 2.800.550.cos 128o
\[ \Rightarrow \] OC2 ≈ 1 484 282, 1
\[ \Rightarrow \] OC ≈ 1 218,3 N (do OC là độ dài đoạn thẳng nên OC > 0)
Suy ra \[\left| {\overrightarrow F } \right|\] ≈ 1 218,3 N.
Vậy độ lớn lực \(\overrightarrow F \) nằm trong khoảng (1 200; 1 300).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Trắc nghiệm Toán 10 Bài 8. Tổng và hiệu của hai vectơ có đáp án !!
Copyright © 2021 HOCTAP247
