Cho tam giác ABC có BC = a, CA = b, AB = c. Hãy tính vecto AB
Câu hỏi :
Cho tam giác ABC có BC = a, CA = b, AB = c. Hãy tính \(\overrightarrow {AB} .\overrightarrow {AC} \) theo a, b, c.
Cho tam giác ABC có BC = a, CA = b, AB = c. Hãy tính \(\overrightarrow {AB} .\overrightarrow {AC} \) theo a, b, c.
A. \[\frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\];
B. \[\frac{{{b^2} + {c^2} - {a^2}}}{4}\];
C. \[{b^2} + {c^2} - {a^2}\];
D. \(\frac{{{b^2} + {c^2} - {a^2}}}{2}\)
* Đáp án
* Hướng dẫn giải
Đáp án đúng là D
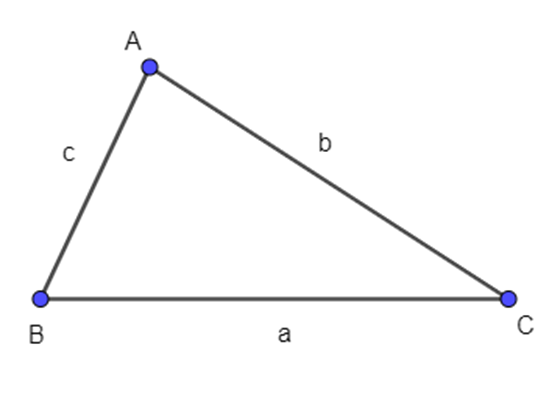
Ta có: \(\overrightarrow {AB} .\overrightarrow {AC} = AB.AC.c{\rm{os}}\left( {\overrightarrow {AB} .\overrightarrow {AC} } \right) = AB.AC.\cos BAC = bc.c{\rm{osBAC}}\)
Theo định lí cos, ta có:
\[{\rm{cosBAC = }}\frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\]
\(\overrightarrow {AB} .\overrightarrow {AC} = bc.\frac{{{b^2} + {c^2} - {a^2}}}{{2bc}} = \frac{{{b^2} + {c^2} - {a^2}}}{2}\).
Vậy \(\overrightarrow {AB} .\overrightarrow {AC} = \frac{{{b^2} + {c^2} - {a^2}}}{2}.\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Trắc nghiệm Toán 10 Bài 11. Tích vô hướng của hai vecto có đáp án !!
Copyright © 2021 HOCTAP247
