Trang chủ
Đề thi & kiểm tra
Lớp 10
Toán học
Trắc nghiệm Toán 10 Bài 17. Dấu của tam thức bậc hai có đáp án !!
Tìm tập xác định của hàm số y = căn...
Tìm tập xác định của hàm số y = căn bậc hai (2x^2 - 5x + 2)
Câu hỏi :
Tìm tập xác định của hàm số \(y = \sqrt {2{x^2} - 5x + 2} \).
Tìm tập xác định của hàm số \(y = \sqrt {2{x^2} - 5x + 2} \).
A. \(D = \left( { - \infty ;\frac{1}{2}} \right]\);
B. D = [2; + ∞);
C. D = \(\left( { - \infty ;\frac{1}{2}} \right] \cup [2; + \infty )\);
D. D = \(\left[ {\frac{1}{2};2} \right]\).
* Đáp án
* Hướng dẫn giải
Đáp án đúng là: C
Hàm số \(y = \sqrt {2{x^2} - 5x + 2} \) xác định khi và chỉ khi 2x2 – 5x + 2 ≥ 0
Xét 2x2 – 5x + 2 = 0 \( \Leftrightarrow \left[ \begin{array}{l}x = \frac{1}{2}\\x = 2\end{array} \right.\)
Ta có bảng xét dấu
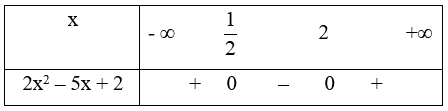
Từ bảng xét dấu ta có 2x2 – 5x + 2 ≥ 0 \(x \in \left( { - \infty ;\frac{1}{2}} \right] \cup \left[ {2; + \infty } \right)\)
Vậy đáp án đúng là C.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Trắc nghiệm Toán 10 Bài 17. Dấu của tam thức bậc hai có đáp án !!
Số câu hỏi: 15
Copyright © 2021 HOCTAP247
