Trang chủ
Đề thi & kiểm tra
Lớp 10
Toán học
Trắc nghiệm Toán 10 Bài tập cuối chương 6 có đáp án !!
Tam thức f(x) = x^2 – 2x – 3 nhận...
Tam thức f(x) = x^2 – 2x – 3 nhận giá trị dương khi và chỉ khi
Câu hỏi :
Tam thức f(x) = x2 – 2x – 3 nhận giá trị dương khi và chỉ khi
Tam thức f(x) = x2 – 2x – 3 nhận giá trị dương khi và chỉ khi
A. x ∈ (– ∞; – 3) \( \cup \) (– 1; + ∞);
B. x ∈ (– ∞; – 1) \( \cup \) (3; + ∞);
C. x ∈ (– ∞; – 2) \( \cup \) (6; + ∞);
D. x ∈ (1; 3).
* Đáp án
* Hướng dẫn giải
Đáp án đúng là: B
Xét f(x) = x2 – 2x – 3 có ∆’ = (–1)2 – 1(–3) = 4 > 0 và a = 1 > 0 nên hàm số có hai nghiệm phân biệt x1 = –1 và x2 = 3.
Khi đó, ta có bảng xét dấu:
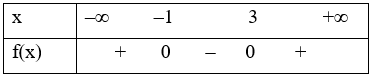
Suy ra f(x) > 0 với x ∈ (– ∞; – 1) \( \cup \) (3; + ∞); f(x) < 0 khi x ∈ (– 1; 3)
Vậy f(x) nhận giá trị dương khi x ∈ (– ∞; – 1) \( \cup \) (3; + ∞).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Trắc nghiệm Toán 10 Bài tập cuối chương 6 có đáp án !!
Số câu hỏi: 60
Copyright © 2021 HOCTAP247
