Cho hình thoi ABCD có độ dài các cạnh bằng 1 và góc DAB = 120^0. Khẳng định nào sau đây là đúng?

* Hướng dẫn giải

Đáp án đúng là: D

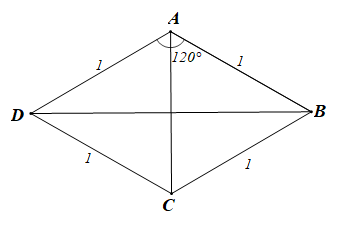
• Xét phương án A:

Vì ABCD là hình thoi nên AB // CD suy ra \(\overrightarrow {AB} = \overrightarrow {DC} .\)

Do đó phương án A là sai.

• Xét phương án B:

Vì ABCD là hình thoi nên hai đường chéo AC và BD vuông góc với nhau.

Khi đó \(\overrightarrow {BD} \bot \overrightarrow {AC} \) nên \[\overrightarrow {BD} \ne \overrightarrow {AC} .\]

Do đó phương án B là sai.

• Xét phương án C:

Vì ABCD là hình thoi có cạnh bằng 1 nên AD = AB = 1.

Xét ABD có AB = AD = 1 và \(\widehat {DAB} = 120^\circ ,\) áp dụng định lí cosin ta có:

BD² = AD² + AB² – 2.AD.AB.cos\(\widehat {DAB}\)

BD² = 1² + 1² – 2.1.1.cos120°

BD² = 3

BD = \(\sqrt 3 \)

Khi đó \(\left| {\overrightarrow {BD} } \right| = BD = \sqrt 3 .\)

Do đó phương án C là sai.

• Xét phương án D:

Vì ABCD là hình thoi có cạnh bằng 1 nên AD = CD = 1 .

Mặt khác \(\widehat {DAB} = 120^\circ \) nên \(\widehat {ADC} = 180^\circ - \widehat {DAB} = 180^\circ - 120^\circ = 60^\circ \)

Tam giác ADC có AD = DC nên là tam giác cân lại có \(\widehat {ADC} = 60^\circ \)

Suy ra ADC là tam giác đều

AC = AD = CD = 1.

Khi đó \(\left| {\overrightarrow {AC} } \right| = AC = 1.\)

Do đó phương án D là đúng.