Cho tam giác ABC có AB = 2, BC = 4 và góc ABC = 60^0. Độ dài của vectơ AC - vecto BA bằng

* Hướng dẫn giải

Đáp án đúng là: C

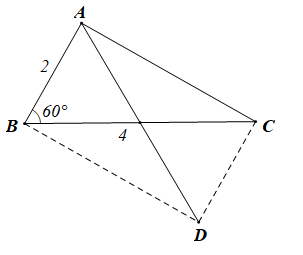
Xét ABC có AB = 2, BC = 4 và \(\widehat {ABC} = 60^\circ .\)

Khi đó tam giác ABC là tam giác vuông tại A.

\( \Rightarrow \widehat {BAC} = 90^\circ .\)

Ta có: \(\overrightarrow {AC} - \overrightarrow {BA} = \overrightarrow {AC} + \overrightarrow {AB} \)

Gọi D là điểm thỏa mãn ABDC là hình bình hành

Khi đó \(\overrightarrow {AC} - \overrightarrow {BA} = \overrightarrow {AC} + \overrightarrow {AB} = \overrightarrow {AD} \)

\[ \Rightarrow \left| {\overrightarrow {AC} - \overrightarrow {BA} } \right| = \left| {\overrightarrow {AD} } \right| = AD\]

Hình bình hành ABDC có \(\widehat {BAC} = 90^\circ \) nên là hình chữ nhật.

Do đó AD = BC (hai đường chéo bằng nhau)

\[ \Rightarrow \left| {\overrightarrow {AC} - \overrightarrow {BA} } \right| = AD = BC = 4.\]

Vậy ta chọn phương án C.