Cho tam giác ABC và điểm I sao cho vecto IB + 2 vecto IC = vecto 0 . Khẳng định nào sau đây là một khẳng định đúng?

* Hướng dẫn giải

Đáp án đúng là: D

Ta có: \(\overrightarrow {IB} + 2\overrightarrow {IC} = \overrightarrow 0 \Rightarrow \overrightarrow {IB} = - 2\overrightarrow {IC} \)

Khi đó \(\overrightarrow {IB} \) và \(\overrightarrow {IC} \) là hai vectơ cùng phương, ngược hướng và IB = 2IC.

Khi đó điểm I nằm giữa hai điểm B và C sao cho IB = 2IC.

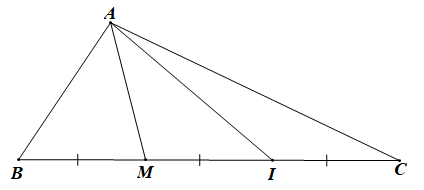
Gọi M là trung điểm của BI.

Khi đó M là trung điểm của BI, I là trung điểm của MC.

Vì I là trung điểm của MC nên ta có:

\(2\overrightarrow {AI} = \overrightarrow {AM} + \overrightarrow {AC} \)(1)

Vì M là trung điểm của BI nên ta có:

\(2\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {AI} \)

\( \Rightarrow \overrightarrow {AM} = \frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AI} \)(2)

Thay (2) vào (1) ta được:

\(2\overrightarrow {AI} = \overrightarrow {AM} + \overrightarrow {AC} \)

\( \Rightarrow 2\overrightarrow {AI} = \left( {\frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AI} } \right) + \overrightarrow {AC} \)

\( \Rightarrow 2\overrightarrow {AI} = \frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AI} + \overrightarrow {AC} \)

\( \Rightarrow 2\overrightarrow {AI} - \frac{1}{2}\overrightarrow {AI} = \frac{1}{2}\overrightarrow {AB} + \overrightarrow {AC} \)

\( \Rightarrow \frac{3}{2}\overrightarrow {AI} = \frac{1}{2}\overrightarrow {AB} + \overrightarrow {AC} \)

\( \Rightarrow \overrightarrow {AI} = \frac{2}{3}.\left( {\frac{1}{2}\overrightarrow {AB} + \overrightarrow {AC} } \right)\)

\( \Rightarrow \overrightarrow {AI} = \frac{{\overrightarrow {AB} + 2\overrightarrow {AC} }}{3}\)

Vậy ta chọn phương án D.