Cho hình vuông ABCD với độ dài cạnh bằng a. Tích vô hướng vecto AB . vecto AC bằng:

* Hướng dẫn giải

Đáp án đúng là: C

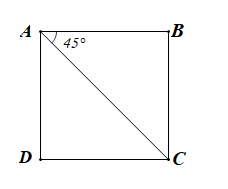
Vì ABCD là hình vuông nên

ABC vuông cân tại B

Do đó:

• \(\widehat {BAC} = 45^\circ \)

• AC = \(\sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \) (theo định lí Pythagore)

Ta có: \(\overrightarrow {AB} .\overrightarrow {AC} \) = AB.AC.cos\[\widehat {BAC}\]

= a.a.\(\sqrt 2 \).cos45°

= a.a\(\sqrt 2 \).\(\frac{{\sqrt 2 }}{2}\)

= a².

Do đó \(\overrightarrow {AB} .\overrightarrow {AC} \) = a².

Vậy ta chọn phương án C.