Cho tam giác ABC có AB = 1, BC = 2 và góc ABC = 60^0. Tích vô hướng vecto BC . vecto CA bằng

* Hướng dẫn giải

Đáp án đúng là: D

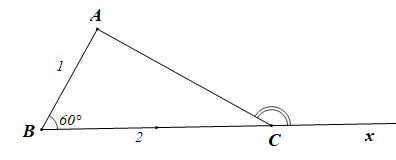
Ta có: \[\overrightarrow {BC} .\overrightarrow {CA} \]= BC.CA.cos\(\left( {\overrightarrow {BC} ,\overrightarrow {CA} } \right)\)

Kéo dài tia BC ta được tia Cx

Khi đó: \(\left( {\overrightarrow {BC} ,\overrightarrow {CA} } \right) = \widehat {ACx}\)

Tam giác ABC có AB = 1, BC = 2

Nên AB = \(\frac{1}{2}\)BC

Lại có \[\widehat {ABC} = 60^\circ .\]

Do đó ABC vuông tại A.

Suy ra:

• AC = \(\sqrt {B{C^2} - A{B^2}} = \sqrt {{2^2} - {1^2}} = \sqrt 3 \)

• \(\widehat {ACB} = 90^\circ - \widehat {ABC} = 90^\circ - 60^\circ = 30^\circ \)

Mà \(\widehat {ACx} = 180^\circ - \widehat {ACB}\) (do hai góc \(\widehat {ACx}\) và \(\widehat {ACB}\) kề bù)

\( \Rightarrow \widehat {ACx} = 180^\circ - 30^\circ = 150^\circ \)

Do đó \[\overrightarrow {BC} .\overrightarrow {CA} \]= BC.CA.cos\(\widehat {ACx}\)

= 2.\(\sqrt 3 \).cos150°

= 2.\(\sqrt 3 .\frac{{ - \sqrt 3 }}{2}\)

= –3.

Vậy ta chọn phương án D.