Cho tam giác ABC vuông tại A với AB = 1, AC = 2. Lấy M, N, P tương ứng thuộc các cạnh BC, CA, AB sao cho 2BM = MC, CN = 2NA, AP = 2PB. Giá trị của tích vô hướng

* Hướng dẫn giải

Đáp án đúng là: C

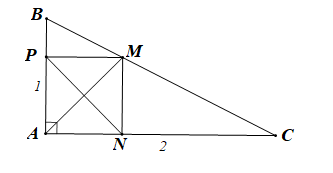
Ta có:

• 2BM = MC \(\frac{{MC}}{{MB}} = \frac{2}{1}\)

• CN = 2NA \(\frac{{CN}}{{NA}} = \frac{2}{1}\)

• AP = 2PB \(\frac{{AP}}{{PB}} = \frac{2}{1}\)

\[ \Rightarrow \frac{{MC}}{{MB}} = \frac{{CN}}{{NA}} = \frac{{AP}}{{PB}}\left( { = \frac{2}{1}} \right)\]

MN // AB và PM // AC (định lí Talet đảo)

ANMP là hình bình hành

Mặt khác:

• \[\frac{{CN}}{{NA}} = \frac{2}{1} \Rightarrow \frac{{CN}}{{NA + CN}} = \frac{2}{{1 + 2}}\]

\(\frac{{CN}}{{CA}} = \frac{2}{3}\)

• MN // AB \(\frac{{MN}}{{AB}} = \frac{{CN}}{{CA}} = \frac{2}{3}\)

MN = \(\frac{2}{3}\).AB = \(\frac{2}{3}\).1 = \(\frac{2}{3}.\)

• \[\frac{{CN}}{{CA}} = \frac{2}{3}\]

CN = \(\frac{2}{3}.\)CA = \(\frac{2}{3}\).2 = \(\frac{4}{3}.\)

AN = CA – CN = 2 – \(\frac{4}{3}\)

AN = \(\frac{2}{3}.\)

Do đó MN = AN = \(\frac{2}{3}.\)

Hình bình hành ANMP có MN = AN nên là hình thoi

Khi đó hai đường chéo AM và PN vuông góc với nhau

\[ \Rightarrow \overrightarrow {AM} \bot \overrightarrow {NP} \]\[ \Rightarrow \overrightarrow {AM} .\overrightarrow {NP} = 0.\]

Vậy ta chọn phương án C.