Cho tam giác ABC đều các cạnh có độ dài bằng 1. Lấy M, N, P lần lượt thuộc các cạnh BC, CA, AB sao cho BM = 2MC, CN = 2NA và AM ⊥ NP. Tỉ số của ( frac{{AP}}{{AB}} ) bằng

* Hướng dẫn giải

Đáp án đúng là: A

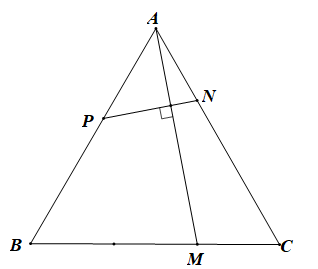
Giả sử

\(\frac{{AP}}{{AB}} = x\) (x > 0)

Ta có:

• Ta có: MB = 2MC nên M nằm giữa B và C

\( \Rightarrow \frac{{BM}}{{MC}} = \frac{2}{1} \Rightarrow \frac{{BM}}{{BM + MC}} = \frac{2}{{2 + 1}}\)

Hay \(\frac{{BM}}{{BC}} = \frac{2}{3} \Rightarrow BM = \frac{2}{3}BC\)

Do đó \(\overrightarrow {BM} = \frac{2}{3}\overrightarrow {BC} \)

Tương tự ta cũng có \(\overrightarrow {AP} = x\overrightarrow {AB} \) và \(\overrightarrow {AN} = \frac{1}{3}\overrightarrow {AC.} \)

• \(\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {BM} \)

\( = \overrightarrow {AB} + \frac{2}{3}\overrightarrow {BC} \)

\[ = \overrightarrow {AB} + \frac{2}{3}\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right)\]

\[ = \overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} - \frac{2}{3}\overrightarrow {AB} \]

\[ = \frac{1}{3}\overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} \]

• \(\overrightarrow {NP} = \overrightarrow {AP} - \overrightarrow {AN} = \overrightarrow {AP} - \frac{1}{3}\overrightarrow {AC} \)

\( = x.\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AC} \)

Mặt khác ta có: AM ⊥ NP

\( \Leftrightarrow \overrightarrow {AM} \bot \overrightarrow {NP} \)

\( \Leftrightarrow \overrightarrow {AM} .\overrightarrow {NP} = 0\)

\[ \Leftrightarrow \left( {\frac{1}{3}\overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} } \right)\left( {x.\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AC} } \right) = 0\]

\[ \Leftrightarrow \frac{1}{3}x.A{B^2} - \frac{1}{9}.\overrightarrow {AB} .\overrightarrow {AC} + \frac{2}{3}x\overrightarrow {AB} .\overrightarrow {AC} - \frac{2}{9}.A{C^2} = 0\]

\[ \Leftrightarrow \frac{1}{3}x.A{B^2} - \frac{1}{9}.\overrightarrow {AB} .\overrightarrow {AC} + \frac{2}{3}x\overrightarrow {AB} .\overrightarrow {AC} - \frac{2}{9}.A{C^2} = 0\] (1)

Tam giác ABC đều có độ dài cạnh bằng 1 nên AB = AC = BC = 1 và \(\widehat {BAC} = 60^\circ .\)

Ta có: \(\overrightarrow {AB} .\overrightarrow {AC} = AB.AC.cos\widehat {BAC}\)

= 1.1.cos60° = \(\frac{1}{2}.\)

Khi đó:

(1) \( \Leftrightarrow \frac{1}{3}.x{.1^2} - \frac{1}{9}.\frac{1}{2} + \frac{2}{3}.x.\frac{1}{2} - \frac{2}{9}{.1^2} = 0\)

\( \Leftrightarrow \frac{2}{3}x = \frac{5}{{18}}\)

\( \Leftrightarrow x = \frac{5}{{18}}:\frac{2}{3} = \frac{5}{{12}}\) (thỏa mãn)

Vậy \(\frac{{AP}}{{AB}} = \frac{5}{{12}}.\)

Ta chọn phương án A.