Cho tam giác ABC. Tập hợp các điểm M thoả mãn | vecto MC - vecto MB| = | vecto MC - vectoAC| là

* Hướng dẫn giải

Đáp án đúng là: A

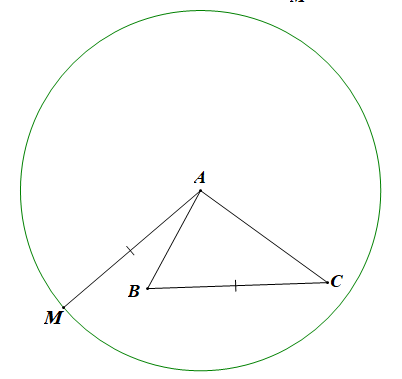
Ta có:

• \[\overrightarrow {MC} --\overrightarrow {MB} = \overrightarrow {BC} \]

• \[\overrightarrow {MC} --\overrightarrow {AC} = \overrightarrow {MC} + \overrightarrow {CA} = \overrightarrow {MA} \]

Khi đó \[\left| {\overrightarrow {MC} --\overrightarrow {MB} } \right| = \left| {\overrightarrow {MC} --\overrightarrow {AC} } \right|\]

\[ \Leftrightarrow \left| {\overrightarrow {BC} } \right| = \left| {\overrightarrow {MA} } \right|\]

BC = MA

Do đó tập hợp điểm M thỏa mãn yêu cầu đề bài là đường tròn tâm A bán kính BC (như hình vẽ trên).

Vậy ta chọn phương án A.