Cho hình bình hành ABCD tâm O. Gọi M, N theo thứ tự là trung điểm của BC, AD. Gọi I, J lần lượt là giao điểm của BD với AM, CN. Xét các vectơ khác vecto 0 , có đầu mút lấy từ cá

* Hướng dẫn giải

Lời giải

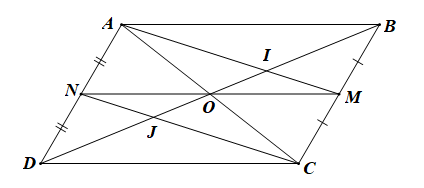
ABCD là hình bình hành có M, N lần lượt là trung điểm của BC, AD

Nên MN là đường trung bình của hình bình hành

MN // AB // DC và MN = AB = DC.

\(\overrightarrow {AB} = \overrightarrow {DC} = \overrightarrow {MN} \)

Vậy những vectơ bằng vectơ \(\overrightarrow {AB} \) là: \(\overrightarrow {AB} ;\overrightarrow {DC} ;\overrightarrow {MN} .\)

Lại có O là tâm hình bình hành nên O là trung điểm của AC và BD

Do đó NO là đường trung bình của ADC

NO // DC

Chứng minh tương tự ta cũng có OM // DC

Do đó ba điểm M, O, N thẳng hàng.

Vậy những vectơ cùng hướng với \(\overrightarrow {AB} \) là: \[\overrightarrow {AB} ,\overrightarrow {NO} ,\overrightarrow {OM} ,\overrightarrow {NM} ,\overrightarrow {DC.} \]