Trên cạnh BC của tam giác ABC lấy các điểm M, N không trùng với B và C sao cho BM = MN =NC.Chứng minh rằng hai tam giác ABC và AMN có cùng trọng tâm.

* Hướng dẫn giải

Lời giải

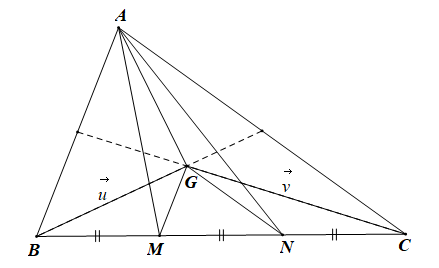
Giả sử G, G' lần lượt là trọng tâm của ABC, AMN.

Sử dụng kết quả của Ví dụ 3, Bài 9 (trang 53, Sách bài tập, Toán 10, Tập một) ta có:

\(\overrightarrow {{\rm{AA}}} + \overrightarrow {BM} + \overrightarrow {CN} = 3\overrightarrow {GG'} \)

\( \Rightarrow \overrightarrow {BM} + \overrightarrow {CN} = 3\overrightarrow {GG'} \)

Mặt khác: M, N lần lượt lấy theo thứ tự trên cạnh BC sao cho BM = MN = NC nên ta có: \(\overrightarrow {BM} = \overrightarrow {MN} = \overrightarrow {NC} \)

\( \Rightarrow \overrightarrow {BM} = - \overrightarrow {CN} \Rightarrow \overrightarrow {BM} + \overrightarrow {CN} = \overrightarrow 0 \)

\( \Rightarrow \overrightarrow {BM} + \overrightarrow {CN} = 3\overrightarrow {GG'} = \overrightarrow 0 \)

Suy ra điểm G và G' trùng nhau.

Do đó hai tam giác ABC và AMN có cùng trọng tâm.