Trên cạnh BC của tam giác ABC lấy các điểm M, N không trùng với B và C sao cho BM = MN =NC.Gọi G là trọng tâm của tam giác ABC.

* Hướng dẫn giải

Lời giải

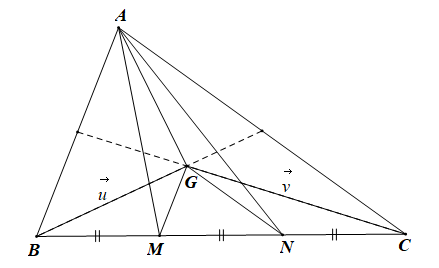
• Vì G là trọng tâm của tam giác ABC nên \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)

\( \Rightarrow \overrightarrow {GA} = - \overrightarrow {GB} - \overrightarrow {GC} \)

\[ \Rightarrow \overrightarrow {GA} = - \overrightarrow u - \overrightarrow v \]

• Từ BM = MN = NC suy ra \(\overrightarrow {MC} = - 2\overrightarrow {MB} \)

Theo Nhận xét ở Ví dụ 2, Bài 9 (trang 53, Sách bài tập, Toán 10, Tập một), với điểm G ta có:

\(\overrightarrow {GC} - \left( { - 2} \right)\overrightarrow {GB} = \left[ {1 - \left( { - 2} \right)} \right]\overrightarrow {GM} \)

\( \Rightarrow 3\overrightarrow {GM} = \overrightarrow {GC} + 2\overrightarrow {GB} \)

\( \Rightarrow \overrightarrow {GM} = \frac{2}{3}\overrightarrow {GB} + \frac{1}{3}\overrightarrow {GC} = \frac{2}{3}\overrightarrow u + \frac{1}{3}\overrightarrow v \)

Tương tự ta cũng có: \(\overrightarrow {GN} = \frac{1}{3}\overrightarrow u + \frac{2}{3}\overrightarrow v \)